
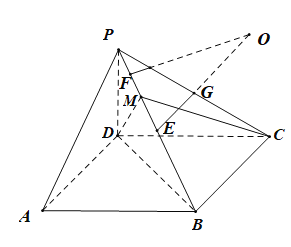
【题目】在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() .以
.以![]() 为直径的球与
为直径的球与![]() 交于点
交于点![]() (异于点
(异于点![]() ),则四面体
),则四面体![]() 外接球半径
外接球半径![]() ______.
______.
【答案】![]()
【解析】
过点![]() 作
作![]() 的垂线,垂足即为
的垂线,垂足即为![]() ,可求出
,可求出![]() ,易证
,易证![]() 平面
平面![]() ,从而可得到平面
,从而可得到平面![]() 平面
平面![]() ,分别取
,分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,可得
,可得![]() ,
,![]() 平面
平面![]() ,由
,由![]() 是直角三角形,可知直线
是直角三角形,可知直线![]() 上任意一点到
上任意一点到![]() 三个顶点的距离相等,作线段
三个顶点的距离相等,作线段![]() 的垂直平方线,垂足为
的垂直平方线,垂足为![]() ,交
,交![]() 于点
于点![]() ,则点
,则点![]() 为三角形
为三角形![]() 的外接圆圆心,且为四面体
的外接圆圆心,且为四面体![]() 外接球球心,由正弦定理可求得三角形
外接球球心,由正弦定理可求得三角形![]() 的外接圆半径,即为所求外接球半径,求解即可.
的外接圆半径,即为所求外接球半径,求解即可.
由题意,![]() 平面
平面![]() ,底面
,底面![]() 为矩形,
为矩形,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,![]() ,
,
过点![]() 作
作![]() 的垂线,垂足即为
的垂线,垂足即为![]() ,
,
![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
则![]() ,
,![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,则
,则![]() ,
,![]() 平面
平面![]() ,
,
因为![]() 是直角三角形,所以直线
是直角三角形,所以直线![]() 上任意一点到
上任意一点到![]() 三个顶点的距离相等,
三个顶点的距离相等,
作线段![]() 的垂直平方线,垂足为
的垂直平方线,垂足为![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 到
到![]() 三个顶点的距离都相等,即四面体
三个顶点的距离都相等,即四面体![]() 外接球球心为
外接球球心为![]() ,且
,且![]() 的外接圆圆心为
的外接圆圆心为![]() ,
,
![]() 中,
中,![]() ,
,
由正弦定理,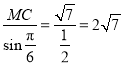 ,即
,即![]() 的外接圆半径为
的外接圆半径为![]() ,四面体
,四面体![]() 外接球半径
外接球半径![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈[0,1],给出以下四个命题:
①平面MENF⊥平面BDD′B′;
②当且仅当x=![]() 时,四边形MENF的面积最小;
时,四边形MENF的面积最小;
③四边形MENF周长L=f(x),x∈[0,1]是单调函数;
④四棱锥C′﹣MENF的体积V=h(x)为常函数;
以上命题中假命题的序号为( )
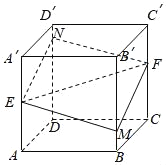
A. ①④B. ②C. ③D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于具有相同定义域D的函数![]() 和
和![]() ,若存在函数
,若存在函数![]() (k,b为常数),对任给的正数m,存在相应的
(k,b为常数),对任给的正数m,存在相应的![]() ,使得当
,使得当![]() 且
且![]() 时,总有
时,总有![]() ,则称直线
,则称直线![]() 为曲线
为曲线![]() 和
和![]() 的“分渐近线”.给出定义域均为
的“分渐近线”.给出定义域均为![]() 的四组函数如下:
的四组函数如下:
①![]() ,
,![]() ;
;
②![]() ,
,![]() ;
;
③![]() ,
,![]() ;
;
④![]() ,
,![]()
其中,曲线![]() 和
和![]() 存在“分渐近线”的是________.
存在“分渐近线”的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区欲建两条圆形观景步道![]() (宽度忽略不计),如图所示,已知
(宽度忽略不计),如图所示,已知![]() ,
,![]() (单位:米),要求圆M与
(单位:米),要求圆M与![]() 分别相切于点B,D,圆
分别相切于点B,D,圆![]() 与
与![]() 分别相切于点C,D.
分别相切于点C,D.
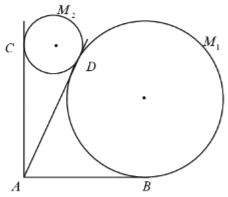
(1)若![]() ,求圆
,求圆![]() 的半径;(结果精确到0.1米)
的半径;(结果精确到0.1米)
(2)若观景步道![]() 的造价分别为每米0.8千元与每米0.9千元,则当
的造价分别为每米0.8千元与每米0.9千元,则当![]() 多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 位数满足下列条件:①各个数字只能从集合
位数满足下列条件:①各个数字只能从集合![]() 中选取;②若其中有数字
中选取;②若其中有数字![]() ,则在
,则在![]() 的前面不含
的前面不含![]() ,将这样的
,将这样的![]() 位数的个数记为
位数的个数记为![]() ;
;
(1)求![]() 、
、![]() ;
;
(2)探究![]() 与
与![]() 之间的关系,求出数列
之间的关系,求出数列![]() 的通项公式;
的通项公式;
(3)对于每个正整数![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() 得到一个新数列
得到一个新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试探究
项和,试探究![]() 能否成立,写出你探究得到的结论并给出证明;
能否成立,写出你探究得到的结论并给出证明;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某芯片公司对今年新开发的一批5G手机芯片进行测评,该公司随机调查了100颗芯片,并将所得统计数据分为![]() 五个小组(所调查的芯片得分均在
五个小组(所调查的芯片得分均在![]() 内),得到如图所示的频率分布直方图,其中
内),得到如图所示的频率分布直方图,其中![]() .
.

(1)求这100颗芯片评测分数的平均数(同一组中的每个数据可用该组区间的中点值代替).
(2)芯片公司另选100颗芯片交付给某手机公司进行测试,该手机公司将每颗芯片分别装在3个工程手机中进行初测。若3个工程手机的评分都达到11万分,则认定该芯片合格;若3个工程手机中只要有2个评分没达到11万分,则认定该芯片不合格;若3个工程手机中仅1个评分没有达到11万分,则将该芯片再分别置于另外2个工程手机中进行二测,二测时,2个工程手机的评分都达到11万分,则认定该芯片合格;2个工程手机中只要有1个评分没达到11万分,手机公司将认定该芯片不合格.已知每颗芯片在各次置于工程手机中的得分相互独立,并且芯片公司对芯片的评分方法及标准与手机公司对芯片的评分方法及标准都一致(以频率作为概率).每颗芯片置于一个工程手机中的测试费用均为300元,每颗芯片若被认定为合格或不合格,将不再进行后续测试,现手机公司测试部门预算的测试经费为10万元,试问预算经费是否足够测试完这100颗芯片?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com