
记函数f(x)的定义域为D,若存在x0∈D,使得f(x)=x成立,则称(x0,x0)为函数f(x)图象上的“稳定点”.
(1)是否存在实数a,使函数f(x)=![]() 的图象上有且仅有两个相异的稳定点?若存在,求出范围;若不存在,请说明理由.
的图象上有且仅有两个相异的稳定点?若存在,求出范围;若不存在,请说明理由.
(2)若函数f(x)是定义在R上的奇函数,求证:函数必有奇数个稳定点.
|
(1)解:设函数f(x)= 则f(x)= 即 所以 解之,得a>5或a<1,a≠- 因此存在a∈(-∞,- (2)证明:因为函数f(x)是定义在R上的奇函数, 所以f(-0)=-f(0),即f(0)=0. 因此(0,0)是f(x)的一个稳定点. 假设函数还有稳定点(x0,x0), 即f(x0)=x0,则必定有f(-x0)=-x0. 这说明(-x0,-x0)也是函数的稳定点. 综上所述,奇函数的稳定点除原点外,都是成对出现,因此其稳定点的个数是奇数. |


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源:2010年江苏省高一第一学期期中考试数学卷 题型:解答题
(满分16分)
记函数f(x)的定义域为D,若存在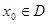 ,使
,使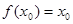 成立,则称以
成立,则称以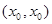 为坐标的点为函数
为坐标的点为函数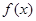 图象上的不动点。
图象上的不动点。
(1)若函数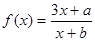 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求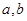 应满足的条件;
应满足的条件;
(2)下述结论“若定义在R上的奇函数f(x)的图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举出一反例说明
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)是否存在实数a,使函数f(x)= ![]() 的图象上有且仅有两个相异的稳定点?若存在,求出范围;若不存在,请说明理由.
的图象上有且仅有两个相异的稳定点?若存在,求出范围;若不存在,请说明理由.
(2)若函数f(x)是定义在R上的奇函数,求证:函数必有奇数个稳定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
(满分16分)记函数f(x)的定义域为D,若存在![]() ,使
,使![]() 成立,则称以
成立,则称以![]() 为坐标的点为函数
为坐标的点为函数![]() 图象上的不动点。
图象上的不动点。
(1)若函数![]() 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求![]() 应满足的条件;
应满足的条件;
(2)下述结论“若定义在R上的奇函数f(x)的图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举出一反例说明。
查看答案和解析>>
科目:高中数学 来源: 题型:
(满分16分)记函数f(x)的定义域为D,若存在![]() ,使
,使![]() 成立,则称以
成立,则称以![]() 为坐标的点为函数
为坐标的点为函数![]() 图象上的不动点。
图象上的不动点。
(1)若函数![]() 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求![]() 应满足的条件;
应满足的条件;
(2)下述结论“若定义在R上的奇函数f(x)的图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举出一反例说明。
(请将解答写在规定的区域,写在其它区域的不得分。)
查看答案和解析>>
科目:高中数学 来源: 题型:
(满分16分)记函数f(x)的定义域为D,若存在![]() ,使
,使![]() 成立,则称以
成立,则称以![]() 为坐标的点为函数
为坐标的点为函数![]() 图象上的不动点。
图象上的不动点。
(1)若函数![]() 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求![]() 应满足的条件;
应满足的条件;
(2)下述结论“若定义在R上的奇函数f(x)的图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举出一反例说明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com