
【题目】已知等差数列![]() 满足:
满足:![]() ,
,![]() .
.![]() 的前n项和为
的前n项和为![]() .
.
(Ⅰ)求![]() 及
及![]() ;
;
(Ⅱ)若![]() ,
,![]() (
(![]() ),求数列
),求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]() =
=![]()
【解析】
试题分析:(Ⅰ)设出首项a1和公差d ,利用等差数列通项公式,就可求出![]() ,再利用等差数列前项求和公式就可求出
,再利用等差数列前项求和公式就可求出![]() ;(Ⅱ)由(Ⅰ)知
;(Ⅱ)由(Ⅰ)知![]() ,再利用
,再利用![]() ,
,![]() (
(![]() ),就可求出
),就可求出![]() ,再利用错位相减法就可求出
,再利用错位相减法就可求出![]() .
.
试题解析:(Ⅰ)设等差数列{an}的首项为a1,公差为d
∵ ![]() ,
,![]() ∴
∴ ![]() 解得
解得 ![]()
∴ ![]()
![]() ,
,
(Ⅱ)∵ ![]() ,
,![]() ∴
∴ ![]()
∵![]() ∴
∴ ![]()
∴ ![]()
![]()
![]()
= ![]() (1-
(1- ![]() +
+ ![]() -
- ![]() +…+
+…+![]() -
-![]() )
)
=![]() (1-
(1-![]() ) =
) =![]()
所以数列![]() 的前
的前![]() 项和
项和![]() =
=![]() .
.
考点:1.等差数列的通项公式; 2. 等差数列的前n项和公式; 3.裂项法求数列的前n项和公式
【题型】解答题
【结束】
18
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
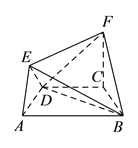
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在线段
)在线段![]() (含端点)上,是否存在一点
(含端点)上,是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,求弦长
两点,求弦长![]() ,若点
,若点![]() ,求
,求![]() 的值;
的值;
(2)以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 和圆
和圆![]() 的交点为
的交点为![]() ,
,![]() ,求弦
,求弦![]() 所在直线的直角坐标方程.
所在直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,其中错误命题有( )
A.单位向量都相等
B.在![]() 中,若
中,若![]() ,则
,则![]() 一定大于
一定大于![]() ;
;
C.若数列![]() 的前
的前![]() 项和为
项和为![]() (
(![]() 、
、![]() 、
、![]() 均为常数),则数列
均为常数),则数列![]() 一定为等差数列;
一定为等差数列;
D.若数列![]() 是等比数列,则数列
是等比数列,则数列![]() 也是等比数列
也是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神舟十号”宇宙飞船进行新产品搭载实验,计划搭载新产品甲,乙,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品甲(件) | 产品乙(件) | ||
研制成本与搭载费用之和(万元/件) | 200 | 300 | 计划最大资金额3000元 |
产品重量(千克/件) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元/件) | 160 | 120 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史,制作工艺十分复杂,它的制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立。某陶瓷厂准备仿制甲、乙、丙三件不同的唐三彩工艺品,根据该厂全面治污后的技术水平,经过第一次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() ,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() .
.
(1)求第一次烧制后甲、乙、丙三件中恰有一件工艺品合格的概率;
(2)经过前后两次烧制后,甲、乙、丙三件工艺品成为合格工艺品的件数为![]() ,求随机变量
,求随机变量![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com