
【题目】如图,在正三棱柱ABCA1B1C1中,F,F1分别是AC,A1C1的中点.
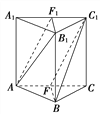
求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
【答案】详见解析
【解析】试题分析:(1)先根据线线平行得线面平行,再根据线面平行得面面平行(2)先证线面垂直:B1F1⊥平面ACC1A1,一根据正三角形性质得B1F1⊥A1C1,二根据正三棱柱性质得B1F1⊥AA1.最后根据面面垂直判定定理得结论
试题解析:(1)在正三棱柱ABCA1B1C1中,
∵F,F1分别是AC,A1C1的中点,
∴B1F1∥BF,AF1∥C1F.
又∵B1F1∩AF1=F1,C1F∩BF=F,
∴平面AB1F1∥平面C1BF.
(2)在正三棱柱ABCA1B1C1中,AA1⊥平面A1B1C1,B1F1平面A1B1C1,
∴B1F1⊥AA1.
又B1F1⊥A1C1,A1C1∩AA1=A1,
∴B1F1⊥平面ACC1A1,而B1F1平面AB1F1,
∴平面AB1F1⊥平面ACC1A1.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时, ![]() ;
;
(1)求函数![]() 在
在![]() 上的解析式并画出函数
上的解析式并画出函数![]() 的图象(不要求列表描点,只要求画出草图)
的图象(不要求列表描点,只要求画出草图)
(2)(ⅰ)写出函数![]() 的单调递增区间;
的单调递增区间;
(ⅱ)若方程![]() 在
在![]() 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 与
与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() ,点
,点![]() 为椭圆的焦点,且
为椭圆的焦点,且![]() 是边长为2的等边三角形,若直线
是边长为2的等边三角形,若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
(1)直线![]() 的斜率之积是否为定值?若是,请求出该定值;若不是,请说明理由;
的斜率之积是否为定值?若是,请求出该定值;若不是,请说明理由;
(2)求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4个不同的球,4个不同的盒子,把球全部放入盒子内.
(1)共有几种放法?
(2)恰有1个空盒,有几种放法?
(3)恰有2个盒子不放球,有几种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年夏季奥运会将在巴西里约热内卢举行,体育频道为了解某地区关于
奥运会直播的收视情况,随机抽取了![]() 名观众进行调查,其中
名观众进行调查,其中![]() 岁以上的观众有
岁以上的观众有![]() 名,下面是根据
名,下面是根据
调查结果绘制的观众准备平均每天收看奥运会直播时间的频率分布表(时间:分钟):
分组 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
将每天准备收看奥运会直播的时间不低于![]() 分钟的观众称为“奥运迷”,已知“奥运迷”中有
分钟的观众称为“奥运迷”,已知“奥运迷”中有![]() 名
名![]() 岁
岁
以上的观众.
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 以上的把握认为“奥运迷”与年龄
以上的把握认为“奥运迷”与年龄
有关?
非“奥运迷” | “奥运迷” | 合计 | |
| |||
| |||
合计 |
(2)将每天准备收看奥运会直播不低于![]() 分钟的观众称为“超级奥运迷”,已知“超级奥运迷”中有
分钟的观众称为“超级奥运迷”,已知“超级奥运迷”中有![]()
名![]() 岁以上的观众,若从“超级奥运迷”中任意选取
岁以上的观众,若从“超级奥运迷”中任意选取![]() 人,求至少有
人,求至少有![]() 名
名![]() 岁以上的观众的概率.
岁以上的观众的概率.
附: 
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(16名女员工,14名男员工)的得分,如下表:
女 | 47 | 36 | 32 | 48 | 34 | 44 | 43 | 47 | 46 | 41 | 43 | 42 | 50 | 43 | 35 | 49 |
男 | 37 | 35 | 34 | 43 | 46 | 36 | 38 | 40 | 39 | 32 | 48 | 33 | 40 | 34 |
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 总计 | |
女 | 16 | ||
男 | 14 | ||
总计 | 30 |
(3)根据上述表中数据,利用独立性检验的方法判断,能否有99%的把握认为该企业员工“性别”与“工作是否满意”有关?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com