
【题目】如图,设长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
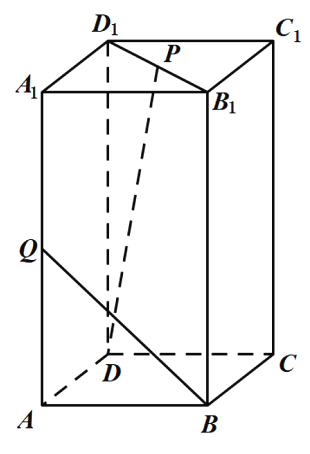
(1)试在线段![]() 上确定点
上确定点![]() 的位置,使得异面直线
的位置,使得异面直线![]() 与
与![]() 所成角为
所成角为![]() ,并请说明你的理由;
,并请说明你的理由;
(2)在满足(1)的条件下,求四棱锥![]() 的体积.
的体积.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】某工厂生产一批零件,为了解这批零件的质量状况,检验员从这批产品中随机抽取了100件作为样本进行检测,将它们的重量(单位:g)作为质量指标值.由检测结果得到如下频率分布直方图.
分组 | 频数 | 频率 |
| 8 | |
| ||
| ||
| 16 | 0.16 |
| 4 | 0.04 |
合计 | 100 | 1 |
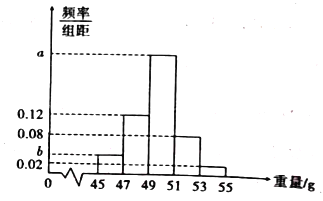
(1)求图中![]() 的值;
的值;
(2)根据质量标准规定:零件重量小于47或大于53为不合格品,重量在区间![]() 和
和![]() 内为合格品,重量在区间
内为合格品,重量在区间![]() 内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该零件重量的概率分布.若这批零件共
内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该零件重量的概率分布.若这批零件共![]() 件
件![]() ,现有两种销售方案:方案一:不再检测其他零件,整批零件除对已检测到的不合格品进行回收处理,其余零件均按150元/件售出;方案二:继续对剩余零件的重量进行逐一检测,回收处理所有不合格品,合格品按150元/件售出,优质品按200元/件售出.仅从获得利润大的角度考虑,该生产商应选择哪种方案?请说明理由.
,现有两种销售方案:方案一:不再检测其他零件,整批零件除对已检测到的不合格品进行回收处理,其余零件均按150元/件售出;方案二:继续对剩余零件的重量进行逐一检测,回收处理所有不合格品,合格品按150元/件售出,优质品按200元/件售出.仅从获得利润大的角度考虑,该生产商应选择哪种方案?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是椭圆
是椭圆![]() 的左焦点,且椭圆
的左焦点,且椭圆![]() 经过点
经过点![]() .
.
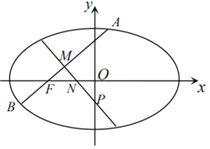
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,过
,过![]() 且与
且与![]() 垂直的直线与
垂直的直线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,记
两点,记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() .若
.若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.

(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?

(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,求这2人都是年龄大于40岁的概率.
附: 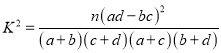 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
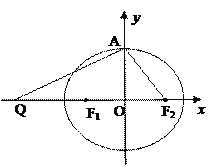
【题目】如图,设椭圆![]() 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且![]() 0,若过 A,Q,F2三点的圆恰好与直线
0,若过 A,Q,F2三点的圆恰好与直线![]() 相切,过定点 M(0,2)的直线
相切,过定点 M(0,2)的直线![]() 与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线
与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线![]() 的斜率
的斜率![]() ,在x轴上是否存在点P(
,在x轴上是否存在点P(![]() ,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出
,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,请说明理由;(Ⅲ)若实数
的取值范围;如果不存在,请说明理由;(Ⅲ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :“双曲线
:“双曲线![]() 任意一点
任意一点![]() 到直线
到直线![]() 的距离分别记作
的距离分别记作![]() ,则
,则![]() 为定值”为真命题.
为定值”为真命题.
(1)求出![]() 的值.
的值.
(2)已知直线![]() 关于y轴对称且使得
关于y轴对称且使得![]() 上的任意点到
上的任意点到![]() 的距离
的距离![]() 满足
满足![]() 为定值,求
为定值,求![]() 的方程.
的方程.
(3)已知直线![]() 是与(2)中某一条直线平行(或重合)且与椭圆
是与(2)中某一条直线平行(或重合)且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 与
与![]() 恰有一个公共点.
恰有一个公共点.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)已知曲线![]() 上两点
上两点![]() ,
,![]() 满足
满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
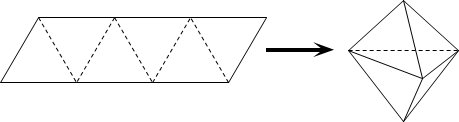
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com