
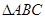 中,内角
中,内角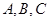 的对边分别为
的对边分别为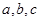 ,已知
,已知 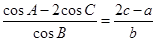
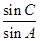 的值;
的值; 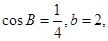 求
求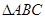 的面积S。
的面积S。科目:高中数学 来源:不详 题型:解答题
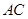 是佛山市一环东线的一段,其中
是佛山市一环东线的一段,其中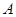 、
、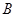 、
、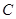 分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界
分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界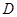 位于点
位于点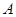 的北偏东
的北偏东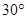 方向
方向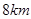 处,位于点
处,位于点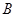 的正北方向,位于点
的正北方向,位于点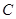 的北偏西
的北偏西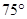 方向上,并且
方向上,并且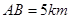 .
.
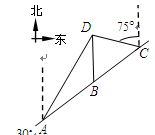
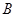 与花卉世界
与花卉世界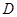 之间的距离;(精确到0.1km)
之间的距离;(精确到0.1km)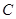 与花卉世界
与花卉世界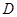 之间的距离.(精确到0.1km)
之间的距离.(精确到0.1km)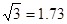 ,
,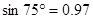 ,
,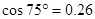 ,
,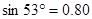 ,
,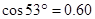 ,
, 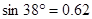 ,
,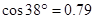
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
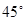 方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南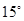 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东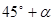 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和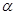 角的正弦值.
角的正弦值.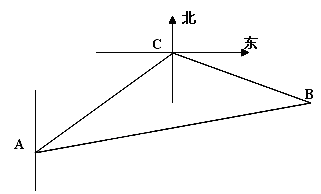
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com