
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证: 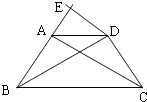
(1)△ABC≌△DCB;
(2)DEDC=AEBD.
【答案】
(1)证明:∵等腰梯形ABCD
∴∠ABC=∠DCB
又∵AB=CD,BC=CB,
∴△ABC≌△DCB
(2)证明:∵△ABC≌△DCB
∴∠ACB=∠DBC,
∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC
∵ED∥AC,∴∠EDA=∠DAC,
∴∠EDA=∠DBC,∠EAD=∠DCB,
∴△ADE∽△CBD
∴DE:BD=AE:CD
∴DEDC=AEBD
【解析】(1)根据梯形为等腰梯形推断出∠ABC=∠DCB,同时根据AB=CD,BC=CB,证明出△ABC≌△DCB.(2)根据(1)中△ABC≌△DCB推断出∠ACB=∠DBC,同时根据AD∥BC和ED∥AC推断出∠EDA=∠DBC,∠EAD=∠DCB,进而根据相似三角形判定定理推断出△ADE∽△CBD,进而根据相似三角形的性质求得DE:BD=AE:CD,推断出DEDC=AEBD.


科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的回归方程 ![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)计算回归系数 ![]() ,
, ![]() .公式为
.公式为  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2, ![]() =λ
=λ ![]() .
. 
(1)若λ=1,求直线DB1与平面A1C1D所成角的正弦值;
(2)若二面角B1﹣A1C1﹣D的大小为60°,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足:an+1=an2﹣nan+1,n=1,2,3,…
(1)当a1=2时,求a2 , a3 , a4并由此猜测an的一个通项公式;
(2)当a1≥3时,证明对所有的n≥1,有
①an≥n+2
② ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2007年到2011年人口总数与年份的关系如表所示
年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据表提供的数据,求最小二乘法求出y关于x的线性回归方程;
(2)据此估计2012年该城市人口总数.
参考公式:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是椭圆
是椭圆![]() 的右焦点,
的右焦点, ![]() 是坐标原点,
是坐标原点, ![]() ,过
,过![]() 作
作![]() 的垂线交椭圆于
的垂线交椭圆于![]() ,
, ![]() 两点,
两点, ![]() 的面积为
的面积为![]() .
.

(1)求该椭圆的标准方程;
(2)若直线![]() 与上下半椭圆分别交于点
与上下半椭圆分别交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求
,求![]() 的面积取得最大值时直线
的面积取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (x∈R).
(x∈R).
(1)求函数f(x)的值域;
(2)①判断函数f(x)的奇偶性;②用定义判断函数f(x)的单调性;
(3)解不等式f(1﹣m)+f(1﹣m2)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com