
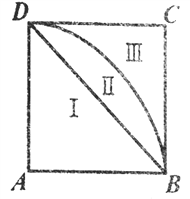
【题目】如图,![]() 是正方形
是正方形![]() 的对角线,弧
的对角线,弧![]() 的圆心是
的圆心是![]() ,半径为
,半径为![]() ,正方形
,正方形![]() 以
以![]() 为轴旋转,求图中Ⅰ,Ⅱ,Ⅲ三部分旋转所得旋转体的体积之比.
为轴旋转,求图中Ⅰ,Ⅱ,Ⅲ三部分旋转所得旋转体的体积之比.
【答案】![]() .
.
【解析】分析:设正方形ABCD的边长为1,可得图Ⅰ旋转所得圆锥的体积为V1=![]() π.图II旋转所得旋转体是半球与图Ⅰ旋转所得圆锥的差,因此它的体积V2=V半球﹣V1=
π.图II旋转所得旋转体是半球与图Ⅰ旋转所得圆锥的差,因此它的体积V2=V半球﹣V1=![]() π.图III旋转所得旋转体是圆柱与半球的差,因此它的体积V3=V圆柱﹣V半球=
π.图III旋转所得旋转体是圆柱与半球的差,因此它的体积V3=V圆柱﹣V半球=![]() π,由此即可得到三部分旋转所得旋转体的体积之比.
π,由此即可得到三部分旋转所得旋转体的体积之比.
详解:
设正方形ABCD的边长为1,可得
图Ⅰ旋转所得旋转体为以AB为轴的圆锥体,高AB=1且底面半径r=1
∴该圆锥的体积为V1=![]() π×AD2×AB=
π×AD2×AB=![]() π;
π;
图II旋转所得旋转体,是以AB为半径的一个半球,减去图Ⅰ旋转所得圆锥体而形成,
∴该圆锥的体积为V2=![]() ×
×![]() π×AB2﹣V1=
π×AB2﹣V1=![]() π﹣
π﹣![]() π=
π=![]() π;
π;
图III旋转所得旋转体,是以AB为轴的圆柱体,减去图II旋转所得半球而形成,
∴该圆锥的体积为V3=π×AD2×AB﹣V半球=π﹣![]() π=
π=![]() π
π
综上所述V1=V2=V3=![]() π,
π,
由此可得图中Ⅰ、Ⅱ、Ⅲ三部分旋转所得旋转体的体积之比为1:1:1.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】(普通班)学校食堂定期从某粮店以每吨 ![]() 元的价格买大米,每次购进大米需支付运输劳务费
元的价格买大米,每次购进大米需支付运输劳务费 ![]() 元,已知食堂每天需要大米
元,已知食堂每天需要大米 ![]() 吨,贮存大米的费用为每吨每天
吨,贮存大米的费用为每吨每天 ![]() 元,假定食堂每次均在用完大米的当天购买.
元,假定食堂每次均在用完大米的当天购买.
(1)该食堂每多少天购买一次大米,能使平均每天所支付的费用最少?
(2)粮店提出价格优惠条件:一次购买量不少于 ![]() 吨时,大米价格可享受九五折优惠(即是原价的
吨时,大米价格可享受九五折优惠(即是原价的 ![]() ),问食堂可否接受此优惠条件?请说明理由.
),问食堂可否接受此优惠条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产不同规格的一种产品,根据检测标准,其合格产品的质量 ![]() 与尺寸
与尺寸 ![]() 之间满足关系式
之间满足关系式 ![]() 为大于
为大于 ![]() 的常数),现随机抽取6件合格产品,测得数据如下:
的常数),现随机抽取6件合格产品,测得数据如下:
对数据作了处理,相关统计量的值如下表:
(1)根据所给数据,求 ![]() 关于
关于 ![]() 的回归方程(提示:由已知,
的回归方程(提示:由已知, ![]() 是
是 ![]() 的线性关系);
的线性关系);
(2)按照某项指标测定,当产品质量与尺寸的比在区间 ![]() 内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率;
内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率;
(附:对于一组数据 ![]() ,其回归直线
,其回归直线 ![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为  )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统综》是明朝程大位所著数学名著,其中有这样一段表述:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一”,其意大致为:有一七层宝塔,每层悬挂的红灯数为上一层的两倍,共有381盏灯,则塔从上至下的第三层有( )盏灯.
A.14
B.12
C.10
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,江的两岸可近似地看出两条平行的直线,江岸的一侧有![]() ,
, ![]() 两个蔬菜基地,江岸的另一侧点
两个蔬菜基地,江岸的另一侧点![]() 处有一个超市.已知
处有一个超市.已知![]() 、
、![]() 、
、![]() 中任意两点间的距离为
中任意两点间的距离为![]() 千米,超市欲在
千米,超市欲在![]() 之间建一个运输中转站
之间建一个运输中转站![]() ,
, ![]() ,
, ![]() 两处的蔬菜运抵
两处的蔬菜运抵![]() 处后,再统一经过货轮运抵
处后,再统一经过货轮运抵![]() 处,由于
处,由于![]() ,
, ![]() 两处蔬菜的差异,这两处的运输费用也不同.如果从
两处蔬菜的差异,这两处的运输费用也不同.如果从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元.从
元.从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元,货轮的运输费为每千米
元,货轮的运输费为每千米![]() 元.
元.

(1)设![]() ,试将运输总费用
,试将运输总费用![]() (单位:元)表示为
(单位:元)表示为![]() 的函数
的函数![]() ,并写出自变量的取值范围;
,并写出自变量的取值范围;
(2)问中转站![]() 建在何处时,运输总费用
建在何处时,运输总费用![]() 最小?并求出最小值.
最小?并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com