
【题目】已知函数f(x)= ![]() x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )
x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:函数f(x)的导数为f'(x)=x+2a, 函数g(x)的导数为 ![]() ,
,
由于两曲线y=f(x),y=g(x)有公共点,设为P(x0 , y0),
则 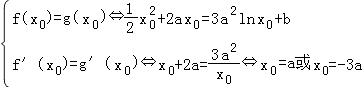 ,
,
由于x0>0,a>0
则x0=a,因此 ![]()
构造函数 ![]() ,
,
由h'(t)=2t(1﹣3lnt),
当 ![]() 时,h'(t)>0即h(t)单调递增;当
时,h'(t)>0即h(t)单调递增;当 ![]() 时,h'(t)<0即h(t)单调递减,
时,h'(t)<0即h(t)单调递减,
则 ![]() 即为实数b的最大值.
即为实数b的最大值.
故选D.
分别求出函数f(x)的导数,函数g(x)的导数.由于两曲线y=f(x),y=g(x)有公共点,
设为P(x0 , y0),则有f(x0)=g(x0),且f′(x0)=g′(x0),解出x0=a,得到b关于a的函数,构造函数 ![]() ,运用导数求出单调区间和极值、最值,即可得到b的最大值.
,运用导数求出单调区间和极值、最值,即可得到b的最大值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立. (I)求该顾客在两次抽奖中恰有一次中奖的概率;
(Ⅱ)记该顾客两次抽奖后的奖金之和为随机变量X,求X的分布列和数学期望.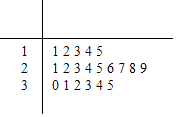
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx+cosx)2+2cos2x
(1)求函数f(x)的最小正周期和单调减区间;
(2)求使f(x)≥3成立的x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=x2﹣(2a+1)x+alnx (Ⅰ) 当a=1时,求函数g(x)的单调增区间;
(Ⅱ) 求函数g(x)在区间[1,e]上的最小值;
(Ⅲ) 在(Ⅰ)的条件下,设f(x)=g(x)+4x﹣x2﹣2lnx,
证明: ![]() >
> ![]() (n≥2).(参考数据:ln2≈0.6931)
(n≥2).(参考数据:ln2≈0.6931)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(3ωx+ ![]() ),其中ω>0
),其中ω>0
(1)若f(x+θ)是周期为2π的偶函数,求ω及θ的值;
(2)若f(x)在(0, ![]() ]上是增函数,求ω的最大值;
]上是增函数,求ω的最大值;
(3)当ω= ![]() 时,将函数f(x)的图象向右平移
时,将函数f(x)的图象向右平移 ![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m=![]() ,n=
,n=![]() .现有如下命题:
.现有如下命题:
①对于任意不相等的实数x1,x2,都有m>0;
②对于任意的a及任意不相等的实数x1,x2,都有n>0;
③对于任意的a,存在不相等的实数x1,x2,使得m=n;
④对于任意的a,存在不相等的实数x1,x2,使得m=-n.
其中的真命题有________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图y=f(x)的导函数的图象,现有四种说法:
(1)f(x)在(﹣3,1)上是增函数;
(2)x=﹣1是f(x)的极小值点;
(3)f(x)在(2,4)上是减函数,在(﹣1,2)上是增函数;
(4)x=2是f(x)的极小值点;
以上正确的序号为( )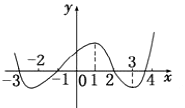
A.(1)(2)
B.(2)(3)
C.(3)(4)
D.(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校拟建一块周长为400m的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽? 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com