
【题目】下列命题错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B. 若![]() 为假命题,则
为假命题,则![]() 均为假命题
均为假命题
C. 对于命题![]() :
:![]()
![]() ,使得
,使得![]() ,则
,则![]() :
:![]()
![]() ,均有
,均有![]()
D. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
【答案】B
【解析】
由原命题与逆否命题的关系即可判断A;由复合命题的真值表即可判断B; 由特称命题的否定是全称命题即可判断C;根据充分必要条件的定义即可判断D;.
A.命题:“若p则q”的逆否命题为:“若¬q则¬p”,故A正确;
B.若p∧q为假命题,则p,q中至少有一个为假命题,故B错.
C.由含有一个量词的命题的否定形式得,命题p:x∈R,使得x2+x+1<0,则¬p为:x∈R,均有x2+x+1≥0,故C正确;
D.由x2﹣3x+2>0解得,x>2或x<1,故x>2可推出x2﹣3x+2>0,但x2﹣3x+2>0推不出x>2,故“x>2”是“x2﹣3x+2>0”的充分不必要条件,即D正确
故选:B.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】某地区为了调查高粱的高度、粒的颜色与产量的关系,对700棵高粱进行抽样调查,得到高度频数分布表如下:
表1:红粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频 数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:白粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频 数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)估计这700棵高粱中红粒高粱的棵数;
(2)估计这700棵高粱中高粱高(![]() )在
)在![]() 的概率;
的概率;
(3)在样本的红粒高粱中,从高度(单位:![]() )在
)在![]() 中任选3棵,设
中任选3棵,设![]() 表示所选3棵中高(单位:
表示所选3棵中高(单位:![]() )在
)在![]() 的棵数,求
的棵数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 (2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )

A.BE∥平面PAD,且BE到平面PAD的距离为![]()
B.BE∥平面PAD,且BE到平面PAD的距离为![]()
C.BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D.BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程以及圆
的普通方程以及圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求线段
两点,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与椭圆
与椭圆![]() 有一个相同的焦点,过点
有一个相同的焦点,过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)试问直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四色猜想是世界三大数学猜想之一,1976年数学家阿佩尔与哈肯证明,称为四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用![]() ,
,![]() ,
,![]() ,
,![]() 四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为
四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为![]() ,粗实线围城的各区域上分别标有数字
,粗实线围城的各区域上分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的四色地图符合四色定理,区域
的四色地图符合四色定理,区域![]() 和区域
和区域![]() 标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为
标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为![]() 的区域的概率所有可能值中,最大的是( )
的区域的概率所有可能值中,最大的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 央视春晚长春分会场,演员身穿独特且轻薄的石墨烯发热服,在寒气逼人的零下
央视春晚长春分会场,演员身穿独特且轻薄的石墨烯发热服,在寒气逼人的零下![]() 春晚现场表演了精彩的节目.石墨烯发热服的制作:从石墨中分离出石墨烯,制成石墨烯发热膜,再把石墨烯发热膜铺到衣服内.
春晚现场表演了精彩的节目.石墨烯发热服的制作:从石墨中分离出石墨烯,制成石墨烯发热膜,再把石墨烯发热膜铺到衣服内.
(1)从石墨分离石墨烯的一种方法是化学气相沉积法,使石墨升华后附着在材料上再结晶。现在有![]() 材料、
材料、![]() 材料供选择,研究人员对附着在
材料供选择,研究人员对附着在![]() 材料上再结晶做了
材料上再结晶做了![]() 次试验,成功
次试验,成功![]() 次;对附着在
次;对附着在![]() 材料上再结晶做了
材料上再结晶做了![]() 次试验,成功
次试验,成功![]() 次.用二列联表判断:是否有
次.用二列联表判断:是否有![]() 的把握认为试验是否成功与材料
的把握认为试验是否成功与材料![]() 和材料
和材料![]() 的选择有关?
的选择有关?
|
| |
成功 | ||
不成功 |
(2)研究人员得到石墨烯后,再制作石墨烯发热膜有四个环节:①透明基底及![]() 胶层;②石墨烯层;③银浆线路;④表面封装层。前三个环节每个环节生产合格的概率为
胶层;②石墨烯层;③银浆线路;④表面封装层。前三个环节每个环节生产合格的概率为![]() ,每个环节不合格需要修复的费用均为
,每个环节不合格需要修复的费用均为![]() 元;第四环节生产合格的概率为
元;第四环节生产合格的概率为![]()
![]() 元,问:一次生产出来的石墨烯发热膜成为合格品平均需要多少修复费用?
元,问:一次生产出来的石墨烯发热膜成为合格品平均需要多少修复费用?
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据史载知,新华网:北京2008年11月9日电,国务院总理温家宝主持召开国务院常务会议,研究部署进一步扩大内需促进经济平稳较快增长的措施,以应对日趋严峻的全球性世界经济金融危机.在提高城乡居民特别是低收入人群的收入水平政策措施的刺激下,某零售店当时近5个月的销售额和利润额数据统计如下表:
月份 | 2 | 3 | 4 | 5 | 6 |
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)若![]() 与
与![]() 之间是线性相关关系,求利润额
之间是线性相关关系,求利润额![]() 关于销售额
关于销售额![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若9月份的销售额为8千万元,试利用(1)的结论估计该零售店9月份的利润额.
参考公式: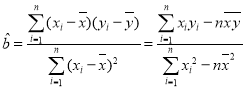 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com