
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的单调增区间;
的单调增区间;
(2)若![]() 恰有三个不同的零点
恰有三个不同的零点![]() (
(![]() ).
).
①求实数![]() 的取值范围;
的取值范围;
②求证:![]() .
.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(1)直接利用导数求函数的单调递增区间. (2)①关于![]() 的方程
的方程![]() 在
在![]() 上有三个不同的解.即关于
上有三个不同的解.即关于![]() 的方程
的方程![]() 在
在![]() 上有三个不同的解.令
上有三个不同的解.令![]() ,
,![]() ,再利用导数研究函数F(x)的图像和值域,即得a的取值范围. ②当
,再利用导数研究函数F(x)的图像和值域,即得a的取值范围. ②当![]() 时,
时,![]() .令
.令![]() ,则
,则![]() ,即
,即![]() ,分析得到
,分析得到![]() ,
,![]() ,代入化简即证
,代入化简即证![]() .
.
(1)当![]() 时,
时,![]() ,定义域为
,定义域为![]() .
.
![]() .
.
所以![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
即![]() 的单调增区间为
的单调增区间为![]() .
.
(2)①由题意可得,关于![]() 的方程
的方程![]() 在
在![]() 上有三个不同的解.
上有三个不同的解.
即关于![]() 的方程
的方程![]() 在
在![]() 上有三个不同的解.
上有三个不同的解.
令![]() ,
,![]() .
.
所以![]() .
.
显然,当![]() 时,
时,![]() ,证明如下:
,证明如下:
令![]() ,
,![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增.
上单调递增.
所以当![]() 时,
时,![]() 取最小值
取最小值![]() .
.
所以,当![]() 时,
时,![]() .
.
令![]() ,可得
,可得![]() 或
或![]() .
.
将x,h1(x),h(x)变化情况列表如下
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
| 极大值 |
|
又当![]()
所以,实数![]() 的取值范围为
的取值范围为![]() .
.
②由①可知,当![]() 时,
时,![]() .
.
令![]() ,则
,则![]() ,
,
即![]() ,
,![]() ,
,![]() .
.
不妨设![]() ,则
,则![]() .
.
又![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
显然,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() ,
,![]() .
.
所以 ![]()
![]()
![]()
![]()
![]()
![]() .
.
即![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分为5组:![]()
![]()
![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
(I)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(II)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
![]()
![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
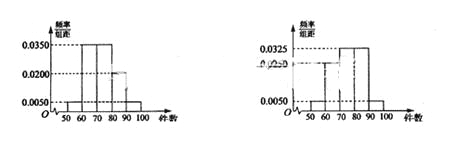
25周岁以上组 25周岁以下组
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计分析,我市城区某拥挤路段的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当该路段的车流密度达到180辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为40千米/小时;当![]() 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度x为多大时,该拥挤路段车流量(单位时间内通过该路段某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为正数,2a2﹣5a1=3,a3a7=9a42;
(1)求数列{an}的通项公式;
(2)设bn=anlog3an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种创新模式,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20 000元,每生产一辆新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数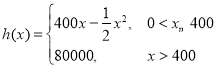 其中x是新样式单车的月产量(单位:辆),利润=总收益-总成本.
其中x是新样式单车的月产量(单位:辆),利润=总收益-总成本.
(1)试将自行车厂的利润y元表示为月产量x的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)若函数![]() 在
在![]() 上恒有意义,求
上恒有意义,求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上为增函数,且最大值为
上为增函数,且最大值为![]() ?若存在求出
?若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com