
【题目】已知数列![]() 满足
满足![]() ,
,![]() .记
.记![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() 时.
时.
(Ⅰ)![]() ;
;
(Ⅱ)![]() ;
;
(Ⅲ)![]() .
.
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)详见解析.
【解析】
(Ⅰ)利用数学归纳法证明,当![]() 时显然成立,假设当
时显然成立,假设当![]() 时不等式成立,即证
时不等式成立,即证![]() 成立即可;
成立即可;
(Ⅱ)要证![]() ,则需证:
,则需证:![]() ,构造函数
,构造函数![]() ,用导数法求函数
,用导数法求函数![]() 的最小值,再由
的最小值,再由![]() 可得结论;
可得结论;
(Ⅲ)先证明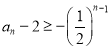 和
和![]() ,再证
,再证 ,结合等比数列的求和公式即可证明
,结合等比数列的求和公式即可证明![]() .
.
证明:(Ⅰ)(1)当![]() 时显然成立;
时显然成立;
(2)假设当![]() 时不等式成立,即
时不等式成立,即![]() ,
,
则![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
设![]() ,
,
则![]() ,∴函数
,∴函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,
,
![]() ,
,
∴![]() ,假设成立,
,假设成立,
综上得,当![]() 时,
时,![]() .
.
(Ⅱ)要证![]() ,即证:
,即证:![]() ,
,
又因为![]() ,则
,则![]() ,
,
则需证:![]() ,
,
由(1)得当![]() 时,
时,![]() ,
,
设![]() ,
,
∵![]() ,
,
∴函数![]() 在
在![]() 上单调递减,而
上单调递减,而![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() .
.
(Ⅲ)由(Ⅱ)可知![]() ,
,
则![]() ,即
,即 ,
,
所以![]() ,
,
则![]() ,
,
∴![]() ,
,
∵![]() ,则
,则![]() ,
,
∴![]() ,
,
即![]() ,所以
,所以![]() ,
,
可知![]() 为等比数列,首项为
为等比数列,首项为![]() ,公比
,公比![]() ,
,
利用等比数列的通项公式得出: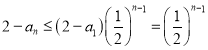 ,
,
∴![]() ,则
,则![]()
![]() ,且
,且![]() ,
,
由题意知![]() ,由于
,由于![]() ,
,
则
![]() ,
,
又因为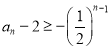 ,且
,且![]() ,
,
则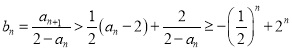 ,
,
则![]() ,
,
由于数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
∴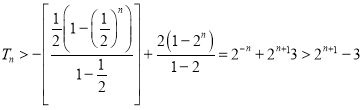 ,
,
即:![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案,决定从2018年秋季入学的高中一年级学生开始实施“![]() ”高考模式.所谓“
”高考模式.所谓“![]() ”,即“3”是指考生必选语文、数学、外语这三科;“1”是指考生在物理、历史两科中任选一科;“2”是指考生在生物、化学、思想政治、地理四科中任选两科.
”,即“3”是指考生必选语文、数学、外语这三科;“1”是指考生在物理、历史两科中任选一科;“2”是指考生在生物、化学、思想政治、地理四科中任选两科.
(1)若某考生按照“![]() ”模式随机选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
”模式随机选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
(2)新冠疫情期间,为积极应对“![]() ”新高考改革,某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果,从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分.
”新高考改革,某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果,从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分.
①考生甲得知他的成绩为270分,考试后不久了解到如下情况:“此次测试平均成绩为171分,351分以上共有57人”,请用你所学的统计知识估计甲能否获得荣誉证书,并说明理由;
②考生丙得知他的实际成绩为430分,而考生乙告诉考生丙:“这次测试平均成绩为201分,351分以上共有57人”,请结合统计学知识帮助丙同学辨别乙同学信息的真伪,并说明理由.
附:![]() ;
;
![]() ;
;
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一个最高点为(![]() ),与之相邻的一个对称中心为
),与之相邻的一个对称中心为![]() ,将f(x)的图象向右平移
,将f(x)的图象向右平移![]() 个单位长度得到函数g(x)的图象,则( )
个单位长度得到函数g(x)的图象,则( )
A.g(x)为偶函数
B.g(x)的一个单调递增区间为![]()
C.g(x)为奇函数
D.函数g(x)在![]() 上有两个零点
上有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x,过点E(a,0)的直线l与C交于不同的两点P(x1,y1),Q(x2,y2),且满足y1y2=﹣4,以Q为中点的线段的两端点分别为M,N,其中N在x轴上,M在C上,则a=_____.|PM|的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为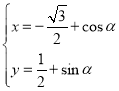 (
(![]() 为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)设射线l的极坐标方程为![]() ,若射线l与曲线C交于A,B两点,求AB的长;
,若射线l与曲线C交于A,B两点,求AB的长;
(2)设M,N是曲线C上的两点,若∠MON![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地出现了虫害,农业科学家引入了“虫害指数”数列![]() ,
,![]() 表示第
表示第![]() 周的虫害的严重程度,虫害指数越大,严重程度越高,为了治理虫害,需要环境整治、杀灭害虫,然而由于人力资源有限,每周只能采取以下两个策略之一:
周的虫害的严重程度,虫害指数越大,严重程度越高,为了治理虫害,需要环境整治、杀灭害虫,然而由于人力资源有限,每周只能采取以下两个策略之一:
策略![]() :环境整治,“虫害指数”数列满足
:环境整治,“虫害指数”数列满足![]() ;
;
策略![]() :杀灭害虫,“虫害指数”数列满足
:杀灭害虫,“虫害指数”数列满足![]() ;
;
当某周“虫害指数”小于1时,危机就在这周解除.
(1)设第一周的虫害指数![]() ,用哪一个策略将使第二周的虫害严重程度更小?
,用哪一个策略将使第二周的虫害严重程度更小?
(2)设第一周的虫害指数![]() ,如果每周都采用最优的策略,虫害的危机最快在第几周解除?
,如果每周都采用最优的策略,虫害的危机最快在第几周解除?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场一年中各月份的收入、支出(单位:万元)情况的统计如折线图所示,则下列说法正确的是( )
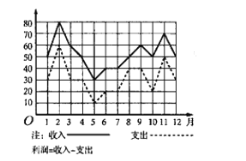
A.2至3月份的收入的变化率与11至12月份的收入的变化率相同
B.支出最高值与支出最低值的比是![]()
C.第三季度平均收入为60万元
D.利润最高的月份是2月份
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
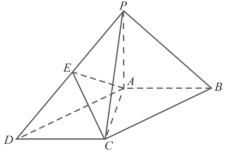
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上(不含端点)是否存在一点
上(不含端点)是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com