
【题目】若对于任意x∈[1,4],不等式0≤ax2+bx+4a≤4x恒成立,|a|+|a+b+25|的范围为_____.
【答案】[25,57]
【解析】
先把不等式变形为﹣b≤a(x![]() )≤4﹣b恒成立,结合f(x)=x
)≤4﹣b恒成立,结合f(x)=x![]() 最值,找到
最值,找到![]() 的限制条件,结合线性规划的知识可得.
的限制条件,结合线性规划的知识可得.
对于任意x∈[1,4],不等式0≤ax2+bx+4a≤4x恒成立,
可得当x∈[1,4]时,不等式﹣b≤a(x![]() )≤4﹣b恒成立,
)≤4﹣b恒成立,
设f(x)=x![]() ,x∈[1,4];
,x∈[1,4];
可得x∈[1,2]时f(x)递减,x∈[2,4]时f(x)递增,
可得![]() 时取得最小值4,
时取得最小值4,![]() 或
或![]() 时取得最大值5,
时取得最大值5,
所以f(x)的值域为[4,5];
所以原不等式恒成立,等价于![]() ,
,
即![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,
所以目标函数z=|a|+|a+b+25|=|y﹣x|+|4x+3y+25|=|y﹣x|+4x+3y+25,
当y≥x时,目标函数z=3x+4y+25,
画出不等式组表示的平面区域,如图,
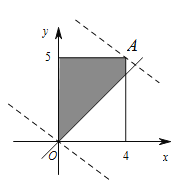
由图可知x=0,y=0时zmin=25,x=4,y=5时zmax=57;
当y<x时,目标函数z=5x+2y+25,如图,

由图可知x=0,y=0时zmin=25,x=4,y=4时zmax=53;
综上可得,|a|+|a+b+25|的范围是[25,57].


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A'B'C',AC=2,BC=4,∠ACB=120°,∠ACC'=90°,且平面AB'C⊥平面ABC,二面角A'﹣AC﹣B'为30°,E、F分别为A'C、B'C'的中点.

(1)求证:EF∥平面AB'C;
(2)求B'到平面ABC的距离;
(3)求二面角A﹣BB'﹣C'的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4坐标系与参数方程选讲
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为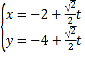 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的平面直角坐标方程和直线
的平面直角坐标方程和直线![]() 的普通方程:
的普通方程:
(2)若![]() 成等比数列,求实数
成等比数列,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数f(x)的最小值为8,求实数a的值;
(Ⅱ)若函数g(x)=|f(x)|+f(x)﹣16有4个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业用180万元购买一套新设备,该套设备预计平均每年能给企业带来100万元的收入,为了维护设备的正常运行,第一年需要各种维护费用10万元,且从第二年开始,每年比上一年所需的维护费用要增加10万元
(1)求该设备给企业带来的总利润![]() (万元)与使用年数
(万元)与使用年数![]() 的函数关系;
的函数关系;
(2)试计算这套设备使用多少年,可使年平均利润最大?年平均利润最大为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() =1(a>b>0)的左焦点分别为F1(-c,0),F2(c,0),过F2作垂直于x轴的直线l交椭圆C于A、B两点,满足|AF2|=
=1(a>b>0)的左焦点分别为F1(-c,0),F2(c,0),过F2作垂直于x轴的直线l交椭圆C于A、B两点,满足|AF2|=![]() c.
c.
(1)椭圆C的离心率;
(2)M、N是椭圆C短轴的两个端点,设点P是椭圆C上一点(异于椭圆C的顶点),直线MP、NP分别和x轴相交于R、Q两点,O为坐标原点,若|OR||OQ|=4,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】混凝土具有原材料丰富、抗压强度高、耐久性好等特点,是目前使用量最大的土木建筑材料抗压强度是混凝土质量控制的重要技术参数,也是实际工程对混凝土要求的基本指标.为了解某型号某批次混凝土的抗压强度(单位: ![]() )随龄期(单位:天)的发展规律,质检部门在标准试验条件下记录了10组混凝土试件在龄期
)随龄期(单位:天)的发展规律,质检部门在标准试验条件下记录了10组混凝土试件在龄期![]() 分别为2,3,4,5,7,9,12,14,17,21时的抗压强度
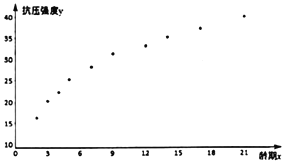
分别为2,3,4,5,7,9,12,14,17,21时的抗压强度![]() 的值,并对数据作了初步处理,得到下面的散点图及一些统计量的值.
的值,并对数据作了初步处理,得到下面的散点图及一些统计量的值.
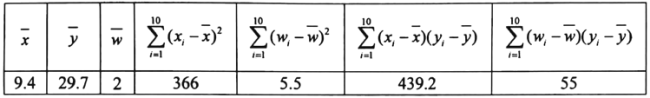
表中![]() ,
,![]() .
.
(1)根据散点图判断![]() 与
与![]() 哪一个适宜作为抗压强度
哪一个适宜作为抗压强度![]() 关于龄期
关于龄期![]() 的回归方程类型?选择其中的一个模型,并根据表中数据,建立
的回归方程类型?选择其中的一个模型,并根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)工程中常把龄期为28天的混凝土试件的抗压强度![]() 视作混凝土抗压强度标准值.已知该型号混凝土设置的最低抗压强度标准值为
视作混凝土抗压强度标准值.已知该型号混凝土设置的最低抗压强度标准值为![]() .
.
(ⅰ)试预测该批次混凝土是否达标?
(ⅱ)由于抗压强度标准值需要较长时间才能评定,早期预测在工程质量控制中具有重要的意义.经验表明,该型号混凝土第7天的抗压强度![]() ,与第28天的抗压强度
,与第28天的抗压强度![]() 具有线性相关关系
具有线性相关关系![]() ,试估计在早期质量控制中,龄期为7天的试件需达到的抗压强度.
,试估计在早期质量控制中,龄期为7天的试件需达到的抗压强度.
附: 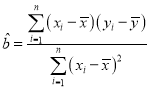 ,
,![]() ,参考数据:
,参考数据: ![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com