
【题目】常州别称龙城,是一座有着3200多年历史的文化古城.常州既有春秋淹城、天宁寺等名胜古迹,又有中华恐龙园、嬉戏谷等游乐景点,每年都有大量游客来常州参观旅游.为合理配置旅游资源,管理部门对首次来中华恐龙园游览的游客进行了问卷调查,据统计,其中![]() 的人计划只游览中华恐龙园,另外
的人计划只游览中华恐龙园,另外![]() 的人计划既游览中华恐龙园又参观天宁寺.每位游客若只游览中华恐龙园,得1分;若既游览中华恐龙园又参观天宁寺,得2分.假设每位首次来中华恐龙园游览的游客均按照计划进行,且是否参观天宁寺相互独立,视频率为概率.
的人计划既游览中华恐龙园又参观天宁寺.每位游客若只游览中华恐龙园,得1分;若既游览中华恐龙园又参观天宁寺,得2分.假设每位首次来中华恐龙园游览的游客均按照计划进行,且是否参观天宁寺相互独立,视频率为概率.
(1)有2名首次来中华恐龙园游览的游客是拼车到常州的,求“这2名游客都是既游览中华恐龙园又参观天宁寺”的概率;
(2)从首次来中华恐龙园游览的游客中随机抽取3人,记这3人的合计得分为X,求X的概率分布和数学期望.
【答案】(1)![]() ;(2)分布列见解析;期望为4.
;(2)分布列见解析;期望为4.
【解析】
(1)根据每位游客只游览中华恐龙园的概率为![]() ,既游览中华恐龙园又参观天宁寺的概率为
,既游览中华恐龙园又参观天宁寺的概率为![]() ,且相互独立,利用独立事件的概率求解.
,且相互独立,利用独立事件的概率求解.
(2)根据每位游客若只游览中华恐龙园,得1分;若既游览中华恐龙园又参观天宁寺,得2分,得到随机变量X的可能取值为3,4,5,6,然后分别求得相应概率,列出分布列再求期望.
(1)由题意,每位游客只游览中华恐龙园的概率为![]() ,既游览中华恐龙园又参观天宁寺的概率为
,既游览中华恐龙园又参观天宁寺的概率为![]()
记两位游客中一位游客“既游览中华恐龙园又参观天宁寺”为事件A,则P(A)=![]() ,
,
另一位游客“既游览中华恐龙园又参观天宁寺”为事件B,则P(B)=![]() ,
,
所以“这2名游客都是既游览中华恐龙园又参观天宁寺”为事件AB,
因为游客是否参观天宁寺相互独立,所以P(AB)=P(A)P(B)=![]() ,
,
(2)随机变量X的可能取值为3,4,5,6,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴X的概率分布为:
X | 3 | 4 | 5 | 6 |
p |
|
|
|
|
所以E(X)=![]() =4.
=4.


科目:高中数学 来源: 题型:
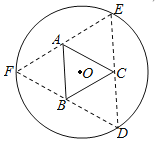
【题目】如图,圆形纸片的圆心为![]() ,半径为
,半径为![]() ,该纸片上的等边三角形
,该纸片上的等边三角形![]() 的中心为
的中心为![]() .
.![]() ,
,![]() ,
,![]() 为圆
为圆![]() 上的点,
上的点,![]() 分别是以
分别是以![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() 为折痕折起
为折痕折起![]() ,使得
,使得![]() ,
,![]() ,
,![]() 重合,得到三棱锥.当所得三棱锥体积(单位:
重合,得到三棱锥.当所得三棱锥体积(单位:![]() )最大时,
)最大时,![]() 的边长为_________(
的边长为_________(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
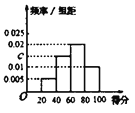
【题目】白塔中学为了解校园爱国卫生系列活动的成效,对全校学生进行了一次卫生意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
(1)求统计表、直方图中的a,b,c的值;
(2)用分层抽样的方法,从等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在某市的一次学情检测中,学生的数学成绩X服从正态分布N(105,100),其中90分为及格线,120分为优秀线,下列说法正确的是( )
附:随机变量![]() 服从正态分布N(
服从正态分布N(![]() ,
,![]() ),则P(
),则P(![]() )=0.6826,P(
)=0.6826,P(![]() )=0.9544,P(
)=0.9544,P(![]() )=0.9974.
)=0.9974.
A.该市学生数学成绩的期望为105
B.该市学生数学成绩的标准差为100
C.该市学生数学成绩及格率超过0.99
D.该市学生数学成绩不及格的人数和优秀的人数大致相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若![]() ,求函数
,求函数![]() 的零点;
的零点;
(2)若不存在相异实数![]() 、
、![]() ,使得
,使得![]() 成立.求实数
成立.求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,总存在实数
,总存在实数![]() 、
、![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
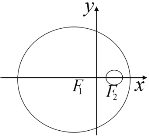
【题目】如图,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若动圆
,若动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过直线![]() 上的点
上的点![]() 作圆
作圆![]() 的两条切线,设切点分别是
的两条切线,设切点分别是![]() ,
,![]() ,若直线
,若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
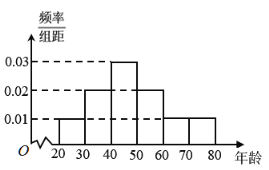
【题目】退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构为了了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在[20,80]内的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示.若规定年龄分布在[60,80]内的人为“老年人”,将上述人口分布的频率视为该城市年龄段在[20,80]的人口分布的概率.从该城市年龄段在[20,80]内的市民中随机抽取3人,记抽到“老年人”的人数为![]() 则随机变量
则随机变量![]() 的数学期望为______.
的数学期望为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com