
【题目】已知数列{an}满足![]() .
.
(1)求a1,a2,a3的值;
(2)对任意正整数n,an小数点后第一位数字是多少?请说明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)a1,a2小数点后第一位数字均为5,当n≥3,n∈N*时,an小数点后第一位数字均为6.见解析
;(2)a1,a2小数点后第一位数字均为5,当n≥3,n∈N*时,an小数点后第一位数字均为6.见解析
【解析】
(1)因为数列{an}满足![]() ,令n=1,n=2,n=3,分别求解.
,令n=1,n=2,n=3,分别求解.
(2)根据a1,a2小数点后第一位数字均为5,a3小数点后第一位数字为6,猜想对任意正整数n(n≥3),均有0.6<an<0.7,根据![]() ,所以对任意正整数n(n≥3),有an≥a3>0.6,只要证明:对任意正整数n(n≥3),有
,所以对任意正整数n(n≥3),有an≥a3>0.6,只要证明:对任意正整数n(n≥3),有![]() 即可.采用数学归纳法证明.
即可.采用数学归纳法证明.
(1)a1![]() ,a2
,a2![]() ;a3
;a3![]() ,
,
可得![]() ,
,![]() ,
,![]() ;
;
(2)a1,a2小数点后第一位数字均为5,a3小数点后第一位数字为6,
下证:对任意正整数n(n≥3),均有0.6<an<0.7,
注意到![]() ,
,
故对任意正整数n(n≥3),有an≥a3>0.6,
下用数学归纳法证明:对任意正整数n(n≥3),有![]()
①当n=3时,有![]() ,命题成立;
,命题成立;
②假设当n=k(k∈N*,k≥3)时,命题成立,即![]()
则当n=k+1时,![]()
∵![]()
∴![]() ∴
∴![]()
∴n=k+1时,命题也成立;
综合①②,任意正整数n(n≥3),![]() .
.
由此,对正整数n(n≥3),0.6<an<0.7,此时an小数点后第一位数字均为6.
所以a1,a2小数点后第一位数字均为5,当n≥3,n∈N*时,an小数点后第一位数字均为6.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,左顶点为
轴上,左顶点为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上每一点的横坐标变为原来的
上每一点的横坐标变为原来的![]() 倍,纵坐标不变,得到曲线
倍,纵坐标不变,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,射线
轴的正半轴为极轴建立极坐标系,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,将射线
,将射线![]() 绕极点逆时针方向旋转
绕极点逆时针方向旋转![]() 交曲线
交曲线![]() 于点
于点![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m<65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到下图的率分布直方图.(同一组数据用该区间的中点值作代表)
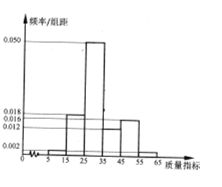
(1)该企业为提高产品质量,开展了质量提升月”活动,活动后再抽样检测,产品三等品数Y近似满足Y~H(10,15,100),请测算“质量提升月”活动后这种产品的“二等品率“(一、二等品其占全部产品百分比)较活动前提高多少个百分点?
(2)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代替相应概率,现有一名联客随机购买两件产品,设其支付的费用为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系x![]() y中,曲线C的参数方程为
y中,曲线C的参数方程为![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴的极坐标系中,直线
轴的非负半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求曲线C的极坐标方程;
(2)设直线![]() 与曲线C相交于A,B两点,P为曲C上的一动点,求△PAB面积的最大值.
与曲线C相交于A,B两点,P为曲C上的一动点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是五四运动100周年.五四运动以来的100年,是中国青年一代又一代接续奋斗、凯歌前行的100年,是中口青年用青春之我创造青春之中国、青春之民族的100年.为继承和发扬五四精神在青年节到来之际,学校组织“五四运动100周年”知识竞赛,竞赛的一个环节由10道题目组成,其中6道A类题、4道B类题,参赛者需从10道题目中随机抽取3道作答,现有甲同学参加该环节的比赛.
(1)求甲同学至少抽到2道B类题的概率;
(2)若甲同学答对每道A类题的概率都是![]() ,答对每道B类题的概率都是
,答对每道B类题的概率都是![]() ,且各题答对与否相互独立.现已知甲同学恰好抽中2道A类题和1道B类题,用X表示甲同学答对题目的个数,求随机变量X的分布列和数学期望.
,且各题答对与否相互独立.现已知甲同学恰好抽中2道A类题和1道B类题,用X表示甲同学答对题目的个数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]()
![]() 有极值,且函数
有极值,且函数![]() 的极值点是
的极值点是![]() 的极值点,其中
的极值点,其中![]() 是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,若函数
时,若函数![]() 的最小值为
的最小值为![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com