
若 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题:
①若 ; ②若
; ②若 ;
;
③若 ; ④若
; ④若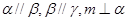 ,则
,则
其中正确命题的个数为
| A.1 | B.2 | C.3 | D.4 |
B
解析考点:平面与平面之间的位置关系;空间中直线与直线之间的位置关系;空间中直线与平面之间的位置关系.
分析:我们可借助正方体去观察理解,①由垂直于平行线中的一条也垂直另一条来判断.②由两平面的位置关系判断.③由两条直线的位置关系判断.④由面面平行的性质定理判断.
解答:解:①∵n∥α,过n作平面β,有α∩β=b,则a∥b,又m⊥α,∴m⊥n,正确.
②若α⊥γ,β⊥γ则α∥β,不正确,可能相交.
③若m∥α,n∥α,则m与n可能平行,相交或异面,所以不正确;
④若α∥β,β∥γ,m⊥α则m⊥γ.由面面平行的性质定理知,正确.
故选B
点评:本题主要考查了两直线,两平面的位置关系,面面平行,线面平行的性质定理,同时,说明特别对于不正确的命题,借助空间几何体更有效.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:河北省2010年高三一模模拟(三)数学理 题型:选择题
若 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,下列命题正确的序号是( )
是三个不同的平面,下列命题正确的序号是( )
①若 则
则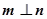 ; ②若
; ②若 ,则
,则 ;[来源:学+科+网Z+X+X+K]
;[来源:学+科+网Z+X+X+K]
③若 则
则 ; ④若
; ④若 ,
,  则
则 .
.
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com