
【题目】如图,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 上的动点,且
上的动点,且![]() ,
,![]() ,
,![]() .
.
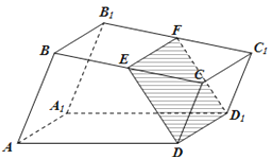
(1)证明:无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)当![]() 时,求几何体
时,求几何体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)要证明无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 为矩形;我们可根据已知中直四棱柱
为矩形;我们可根据已知中直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() 分别是
分别是![]() 上的动点,且
上的动点,且![]() ,先由线面平行的性质定理,判断出四边形
,先由线面平行的性质定理,判断出四边形![]() 为平行四边形,再证明其邻边相互垂直,进而得到答案;(2)连接
为平行四边形,再证明其邻边相互垂直,进而得到答案;(2)连接![]() ,我们易根据已知条件,结合直棱柱的几何特征和勾股定理,判断出
,我们易根据已知条件,结合直棱柱的几何特征和勾股定理,判断出![]() 到为四棱锥的高,根据
到为四棱锥的高,根据![]() 及
及![]() ,我们计算出四棱锥面面积的和高,代入棱锥体积公式即可得到答案.
,我们计算出四棱锥面面积的和高,代入棱锥体积公式即可得到答案.
(1)在直四棱柱![]() 中,
中,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∵侧棱![]() 底面
底面![]() ,又
,又![]() 平面
平面![]() 内,
内,
∴![]() ,∴四边形
,∴四边形![]() 为矩形;
为矩形;
(2)证明:连结![]() ,∵四棱柱
,∵四棱柱![]() 为直四棱柱,
为直四棱柱,
∴侧棱![]() 底面
底面![]() ,又
,又![]() 平面
平面![]() 内,∴
内,∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ;
;
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ;
;
在直角梯形中![]() ,
,![]() ;
;
∴![]() ,即
,即![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ;
;
由(Ⅰ)可知,四边形![]() 为矩形,且
为矩形,且![]() ,
,![]() ,
,
∴矩形![]() 的面积为
的面积为![]() ,
,
∴几何体![]() 的体积为
的体积为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某市2019年引进天然气作为能源,并将该项目工程承包给中昱公司.已知中昱公司为该市铺设天然气管道的固定成本为35万元,每年的管道维修此用为5万元.此外,该市若开通![]() 千户使用天然气用户
千户使用天然气用户![]() ,公司每年还需投入成本
,公司每年还需投入成本![]() 万元,且
万元,且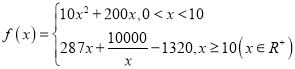 .通过市场调研,公司决定从每户天然气新用户征收开户费用2500元,且用户开通天然气后,公司每年平均从每户使用天然气的过程中获利360元.
.通过市场调研,公司决定从每户天然气新用户征收开户费用2500元,且用户开通天然气后,公司每年平均从每户使用天然气的过程中获利360元.
(1)设该市2019年共发展使用天然气用户![]() 千户,求中昱公司这一年利润
千户,求中昱公司这一年利润![]() (万元)关于
(万元)关于![]() 的函数关系式;
的函数关系式;
(2)在(1)的条件下,当![]() 等于多少
等于多少![]() 最大?且
最大?且![]() 最大值为多少?
最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆上的一个动点(不与左、右顶点重合),且
是椭圆上的一个动点(不与左、右顶点重合),且![]() 的周长为6,点
的周长为6,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,直线
,直线![]() 交于点
交于点![]() .
.
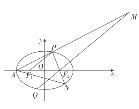
(1)求椭圆方程;
(2)若直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ,η,已知甲、乙两名射手在每次射击中射中的环数大于6环,且甲射中10,9,8,7环的概率分别为0.5,3a,a,0.1,乙射中10,9,8环的概率分别为0.3,0.3,0.2.
(1)求ξ,η的分布列;
(2)求ξ,η的数学期望与方差,并以此比较甲、乙的射击技术.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com