
【题目】函数fn(x)=xn+bx+c(n∈Z,b,c∈R).
(1)若n=﹣1,且f﹣1(1)=f﹣1(![]() )=5,试求实数b,c的值;
)=5,试求实数b,c的值;
(2)设n=2,若对任意x1,x2∈[﹣1,1]有|f2(x1)﹣f2(x2)|≤6恒成立,求b的取值范围.
【答案】(1)b=3,c=1;(2)﹣3≤b≤3.
【解析】
(1)由条件可得![]() ,
,![]() 的方程,解方程可得
的方程,解方程可得![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() ,对任意
,对任意![]() ,
,![]() ,
,![]() 有
有![]() 恒成立等价于
恒成立等价于![]() 在
在![]() ,
,![]() 上的最大值与最小值之差
上的最大值与最小值之差![]() .讨论对称轴和区间的关系,判断单调性,可得最值,解不等式即可得到所求范围.
.讨论对称轴和区间的关系,判断单调性,可得最值,解不等式即可得到所求范围.
(1)n=﹣1时,f﹣1(x)=x﹣1+bx+c,
且f﹣1(1)=f﹣1(![]() )=5,
)=5,
可得1+b+c=5,3![]() b+c=5,解得b=3,c=1;
b+c=5,解得b=3,c=1;
(2)当n=2时,f2(x)=x2+bx+c,
对任意x1,x2∈[﹣1,1]有|f2(x1)﹣f2(x2)|≤6恒成立等价于
f2(x)在[﹣1,1]上的最大值与最小值之差M≤6.
①当![]() 1,即b>2时,f2(x)在[﹣1,1]递增,
1,即b>2时,f2(x)在[﹣1,1]递增,
f2(x)min=f2(﹣1)=1﹣b+c,f2(x)max=f2(1)=1+b+c,
M=2b>4,且2b≤6,可得2<b≤3;
②当﹣1![]() 0,即0≤b≤2时,f2(x)在[﹣1,
0,即0≤b≤2时,f2(x)在[﹣1,![]() ]递减,在(
]递减,在(![]() ,1]递增,
,1]递增,
f2(x)min=f2(![]() )=c
)=c![]() ,f2(x)max=f2(1)=1+b+c,M=(
,f2(x)max=f2(1)=1+b+c,M=(![]() 1)2≤6恒成立,故0≤b≤2;
1)2≤6恒成立,故0≤b≤2;
③当0![]() 1即﹣2≤b<0时,f2(x)在[﹣1,
1即﹣2≤b<0时,f2(x)在[﹣1,![]() ]递减,在(
]递减,在(![]() ,1]递增,
,1]递增,
f2(x)min=f2(![]() )=c
)=c![]() ,f2(x)max=f2(﹣1)=1﹣b+c,M=(
,f2(x)max=f2(﹣1)=1﹣b+c,M=(![]() 1)2≤6恒成立,故﹣2≤b<0;
1)2≤6恒成立,故﹣2≤b<0;
④当![]() 1,即b<﹣2时,f2(x)在[﹣1,1]递减,
1,即b<﹣2时,f2(x)在[﹣1,1]递减,
f2(x)min=f2(1)=1+b+c,f2(x)max=f2(﹣1)=1﹣b+c,
M=﹣2b>4且﹣2b≤6,可得﹣3≤b<﹣2.
综上可得,b的取值范围是﹣3≤b≤3.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与
的图象与![]() 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为![]() ,且图象过点
,且图象过点![]()
(1)求![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() ,在区间
,在区间![]() 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地一天从![]() 时的温度变化曲线近似满足函数
时的温度变化曲线近似满足函数![]() .
.
(1)求该地区这一段时间内温度的最大温差.
(2)若有一种细菌在![]() 到
到![]() 之间可以生存,则在这段时间内,该细菌最多能存活多长时间?
之间可以生存,则在这段时间内,该细菌最多能存活多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在其定义域内存在实数
,若在其定义域内存在实数![]() 满足
满足![]() ,则称函数
,则称函数![]() 为“局部奇函数”,若函数
为“局部奇函数”,若函数![]() 是定义在
是定义在![]() 上的“局部奇函数”,则实数
上的“局部奇函数”,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第二届乌镇互联网大会中, 为了提高安保的级别同时又为了方便接待,现将其中的五个参会国的人员安排酒店住宿,这五个参会国要在![]() 、
、![]() 、
、![]() 三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有
三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有
A.![]() 种B.
种B.![]() 种
种
C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲题型:给出如图数阵表格形式,表格内是按某种规律排列成的有限个正整数.
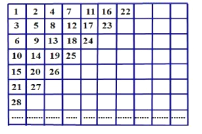
(1)记第一行的自左至右构成数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,试求;
项和,试求;
(2)记![]() 为第
为第![]() 列第
列第![]() 行交点的数字,观察数阵请写出
行交点的数字,观察数阵请写出![]() 表达式,若
表达式,若![]() ,试求出
,试求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com