
【题目】设函数f (x)的导函数为f′(x),对任意x∈R都有f (x)>f′(x)成立,则( )
A.3f (ln2)<2 f (ln3)
B.3 f (ln2)=2 f (ln3)
C.3 f(ln2)>2 f (ln3)
D.3 f (ln2)与2 f (ln3)的大小不确定
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,M,N分别为AB,BC的中点.
(1)求证:平面B1MN⊥平面BB1D1D;
(2)当点P在DD1上运动时,是否都有MN∥平面A1C1P,证明你的结论;
(3)若P是D1D的中点,试判断PB与平面B1MN是否垂直?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C:ρ2﹣2ρcosθ﹣8=0 曲线E: ![]() (t是参数)
(t是参数)
(1)求曲线C的普通方程,并指出它是什么曲线.
(2)当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ,g(x)=﹣x﹣ln(﹣x)其中a≠0,
,g(x)=﹣x﹣ln(﹣x)其中a≠0,
(1)若x=1是函数f(x)的极值点,求实数a的值及g(x)的单调区间;
(2)若对任意的x1∈[1,2],x2∈[﹣3,﹣2]使得f(x1)≥g(x2)恒成立,且﹣2<a<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=lnf′(x)的单调减区间为( ) 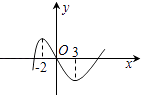
A.[0,3)
B.[﹣2,3]
C.(﹣∞,﹣2)
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体对“男女同龄退休”这一公众关注的问题进行 了民意调査,右表是在某单位得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
附表:
P(K2≥K) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
(1 )能否有90%以上的把握认为对这一问题的看法与性别有关?
【答案】解:解:K2= ![]() ≈2.932>2.706,
≈2.932>2.706,
由此可知,有90%的把握认为对这一问题的看法与性别有关
(1)进一步调查:(ⅰ)从赞同“男女同龄退休”16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率; (ⅱ)从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com