解下列不等式:
(1)19x-3x2≥6;
(2)0<x2-x-2≤4.
解:(1)由原不等式,得-3x
2+19x-6≥0,可化为:
3x
2-19x+6≤0,
∴不等式3x
2-19x+6≤0的解集为{x|

≤x≤6}.
∴原不等式的解集为{x|

≤x≤6}.
(2)不等式0<x
2-x-2≤4可化为:
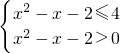
,
即
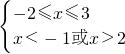
∴x∈[-2,-1)∪(2,3],
∴原不等式的解集为[-2,-1)∪(2,3].
分析:(1)应用解一元二次不等式的步骤、方法解答即可:首先将原不等式转化成二次项系数为正数的不等式,而后判断对应方程的判别式,看方程实数根的情况,最后根据二次函数的开口方向确定原不等式的解集.
(2)转化二次不等式为不等式组,然后求解即可.
点评:解一元二次不等式是高中数学经常遇到的问题,应当按照解一元二次不等式的步骤、方法解答并熟练掌握.

 ≤x≤6}.
≤x≤6}. ≤x≤6}.
≤x≤6}.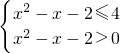 ,
,