
(本小题满分8分) 某车间生产某机器的两种配件A和B,生产配件A成本费y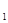 与该车间的工人人数x成反比,而生产配件B成本费y
与该车间的工人人数x成反比,而生产配件B成本费y 与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y
与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y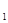 和y
和y 分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某工厂生产一种产品,已知该产品的月产量x吨与每吨产品的价格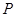 (元)之间的关系为
(元)之间的关系为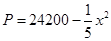 ,且生产
,且生产 吨的成本为
吨的成本为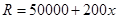 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了应对国际原油的变化,某地建设一座油料库。现在油料库已储油料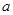 吨,计划正式运营后的第一年进油量为已储油量的
吨,计划正式运营后的第一年进油量为已储油量的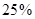 ,以后每年的进油量为上一年年底储油量的
,以后每年的进油量为上一年年底储油量的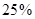 ,且每年运出
,且每年运出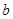 吨,设
吨,设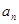 为正式运营第n年年底的储油量。(其中
为正式运营第n年年底的储油量。(其中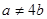 )
)
(1)求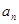 的表达式
的表达式
(2)为应对突发事件,该油库年底储油量不得少于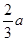 吨,如果
吨,如果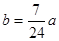 吨,该油库能否长期按计划运营?如果可以请加以证明;如果不行请求出最多可以运营几年。(取
吨,该油库能否长期按计划运营?如果可以请加以证明;如果不行请求出最多可以运营几年。(取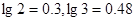 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分)
已知函数f (x)=| x-a | + | x + 2 |(a为常数,且a∈R).
(Ⅰ)若函数f (x)的最小值为2,求a的值;
(Ⅱ)当a=2时,解不等式f (x)≤6.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com