
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{11}{12}$ | D. | $\frac{1}{18}$ |
分析 本题是一个等可能事件的概率,试验发生包含的事件是点数对(a,b)共有6×6对,不满足条件的事件向量$\overrightarrow{m}$与向量$\overrightarrow{n}$不共线,即向量$\overrightarrow{m}$与向量$\overrightarrow{n}$共线时2a-b=0,即b=2a,共3种情况,进而根据对立事件概率减法公式,可得答案.
解答 由题意知本题是一个等可能事件的概率,
试验发生包含的事件是点数对(a,b)共有6×6=36对,
满足条件的事件是向量$\overrightarrow{m}$与向量$\overrightarrow{n}$不共线,即2a-b≠0,
由满足2a-b=0的事件有(1,2),(2,4),(3,6)共3种,
故向量$\overrightarrow{m}$与向量$\overrightarrow{n}$共线的概率为:$\frac{3}{36}$=$\frac{1}{12}$,
故向量$\overrightarrow{m}$与向量$\overrightarrow{n}$不共线的概率P=1-$\frac{1}{12}$=$\frac{11}{12}$,
故选:C
点评 本题考查的知识点是古典概型,向量平行的充要条件,是向量与概率的综合应用.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{e}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 1或$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期为2π的奇函数 | B. | 周期为$\frac{π}{2}$的奇函数 | ||
| C. | 周期为π的偶函数 | D. | 周期为2π的偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
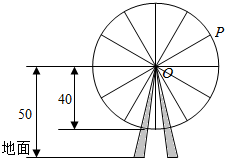 如图,摩天轮的半径为40m,摩天轮的圆心O距地面为50m,且摩天轮做匀速转动,每3min转-圈,摩天轮上的点P的起始位置在最低点处,若在时刻t(单位:min)时点P距离地面的高度f(t)=Asin(ωt+φ)+h(A>0,ω>0,|φ|≤$\frac{π}{2}$),求2014min时,点P距离地面的高度.
如图,摩天轮的半径为40m,摩天轮的圆心O距地面为50m,且摩天轮做匀速转动,每3min转-圈,摩天轮上的点P的起始位置在最低点处,若在时刻t(单位:min)时点P距离地面的高度f(t)=Asin(ωt+φ)+h(A>0,ω>0,|φ|≤$\frac{π}{2}$),求2014min时,点P距离地面的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com