
分析 设圆锥的母线为l,底面半径为r,由已知条件求出l=3,r=1,从而求出圆锥的高,由此能求出圆锥的体积.
解答 解:设圆锥的母线为l,底面半径为r,
∵3π=$\frac{1}{3}$πl2,∴l=3,
∴120°=$\frac{r}{3}$×360°,
∴r=1,
∴圆锥的高是$\sqrt{9-1}$=2$\sqrt{2}$,
∴圆锥的体积是$\frac{1}{3}$×π×12×2$\sqrt{2}$=$\frac{2\sqrt{2}}{3}π$.
故答案为:$\frac{2\sqrt{2}}{3}π$.
点评 本题考查圆锥的体积的求法,是中档题,解题时要认真审题,注意圆锥的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 科目选择 | 物理 化学 生物 | 历史 地理 政治 | 物理 化学 地理 | 历史 地理 生物 | 物理 政治 历史 | 其他 |
| 频率 | $\frac{1}{5}$ | $\frac{1}{6}$ | $\frac{2}{15}$ | a | b | c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
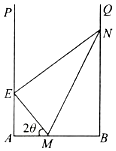 某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.
某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<3} | B. | {-1,0,1} | C. | {x|-1<x<2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 节 气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
| 晷影 长 (寸) | 135.0 | $125.\frac{5}{6}$ | $115.1\frac{4}{6}$ | $105.2\frac{3}{6}$ | $95.3\frac{2}{6}$ | $85.4\frac{2}{6}$ | 75.5 | $66.5\frac{5}{6}$ | $55.6\frac{4}{6}$ | $45.7\frac{3}{6}$ | $35.8\frac{2}{6}$ | $25.9\frac{1}{6}$ | 16.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com