
【题目】给出下列四个命题:
(1函数f(x)=loga(2x﹣1)﹣1的图象过定点(1,0);
(2化简2 ![]() +lg5lg2+(lg2)2﹣lg2的结果为25;
+lg5lg2+(lg2)2﹣lg2的结果为25;
(3若loga ![]() <1,则a的取值范围是(1,+∞);
<1,则a的取值范围是(1,+∞);
(4若2﹣x﹣2y>lnx﹣ln(﹣y)(x>0,y<0),则x+y<0.
其中所有正确命题的序号是
【答案】(2)(4)
【解析】解:(1)函数f(x)=loga(2x﹣1)﹣1的图象过定点(1,﹣1),故(1)错误;(2)2 ![]() +lg5lg2+(lg2)2﹣lg2=25+lg2(lg5+lg2)﹣lg2=25+lg2﹣lg2=25,故(2)正确;(3)若loga
+lg5lg2+(lg2)2﹣lg2=25+lg2(lg5+lg2)﹣lg2=25+lg2﹣lg2=25,故(2)正确;(3)若loga ![]() <1,则a的取值范围是(0,
<1,则a的取值范围是(0, ![]() )∪(1,+∞),故(3)错误;(4)构造函数F(t)=2﹣t﹣lnt,t∈(0,+∞),
)∪(1,+∞),故(3)错误;(4)构造函数F(t)=2﹣t﹣lnt,t∈(0,+∞),
显然,F(t)为定义域上的减函数,
因为x>0,y<0,所以,﹣y>0,
故F(x)=2﹣x﹣lnx,F(﹣y)=2y﹣ln(﹣y),
由①式得,F(x)>F(﹣y),
且F(t)为定义域上的减函数,
因此,x<﹣y,
即x+y<0,故(4)正确;
所以答案是:(2)(4)
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:高中数学 来源: 题型:
【题目】若函数f(x)=ax+ka﹣x(a>0且a≠1)在R上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.
B.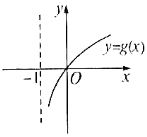
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:实数x满足x2﹣4ax+3a2<0,其中a>0; q:实数x满足2<x≤3.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比不为1的等比数列{an}的前5项积为243,且2a3为3a2和a4的等差中项.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=bn﹣1log3an+2(n≥2且n∈N*),且b1=1,求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若c-b=2bcosA.
(1)求证:A=2B;
(2)若cosB=![]() ,c=5,求△ABC的面积.
,c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(16x+k)﹣2x (k∈R)是偶函数.
(1)求k;
(2)若不等式m﹣1≤f(x)≤2m+log217在x∈[﹣1, ![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com