
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,且
,且![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)过点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,
两点,![]() 都在
都在![]() 轴上方,并且
轴上方,并且![]() 在
在![]() 之间,且
之间,且![]() 到直线
到直线![]() 的距离是
的距离是![]() 到直线
到直线![]() 距离的
距离的![]() 倍.
倍.
①记![]() 的面积分别为
的面积分别为![]() ,求
,求![]() ;
;
②若原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求椭圆方程.
,求椭圆方程.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
试题本题以直线与椭圆的位置关系为背景.第(1)小题设计为求椭圆的离心率,只需利用条件![]() 是
是![]() 的中点,可得
的中点,可得![]() ,从而得
,从而得![]() .第(2)小题中第①题求
.第(2)小题中第①题求![]() ,需要用等积法进行转化,即
,需要用等积法进行转化,即![]() .第②题求椭圆方程,设直线
.第②题求椭圆方程,设直线![]() 方程为
方程为![]() .注意到
.注意到![]() ,和原点
,和原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() ,从而可以确定
,从而可以确定![]() ,
,![]() ,
,![]() 的值.
的值.
试题解析:(1)因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,即
,即![]() ,又
,又![]() 、
、![]() ,
,
所以![]() ,所以
,所以![]() ;
;
(2)①解法一:过![]() 作直线
作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,依题意,
,依题意,![]() ,
,
又![]() ,故
,故![]() ,故
,故![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() 是
是![]() 中点,∴
中点,∴![]() ,∴
,∴![]() ;
;
解法二:∵![]() ,∴
,∴![]() ,椭圆方程为
,椭圆方程为![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,即有
上,即有![]() ,
,
![]()
![]()
同理![]() ,
,
又![]() ,故
,故![]() 得
得![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() 是
是![]() 中点,∴
中点,∴![]() ,∴
,∴![]() ;
;
②解法一:设![]() ,则椭圆方程为
,则椭圆方程为![]() ,
,
由①知![]() 是
是![]() 的中点,不妨设
的中点,不妨设![]() ,则
,则![]() ,
,
又![]() 都在椭圆上,即有
都在椭圆上,即有![]()
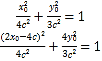 即
即![]()
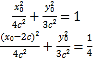
两式相减得:![]() ,解得
,解得![]() ,
,
可得![]() ,故直线
,故直线![]() 的斜率为
的斜率为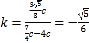 ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]()
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
依题意![]() ,解得
,解得![]() ,故椭圆方程为
,故椭圆方程为![]() .
.
解法二:设![]() ,则椭圆方程为
,则椭圆方程为![]() ,
,
由①知![]() 是
是![]() 的中点,故
的中点,故![]() ,
,
直线![]() 的斜率显然存在,不妨设为
的斜率显然存在,不妨设为![]() ,故其方程为
,故其方程为![]() ,与椭圆联立,并消去
,与椭圆联立,并消去![]() 得:
得:![]() ,整理得:
,整理得:![]() ,(*)
,(*)
设![]() ,
,![]() ,依题意:
,依题意:![]()
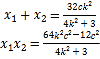 ]
]
由![]()
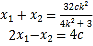 解得:
解得:![]()

所以![]() ,解之得:
,解之得:![]() ,即
,即![]() .
.
直线![]() 的方程为
的方程为![]() ,即
,即![]()
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
依题意![]() ,解得
,解得![]() ,故椭圆方程为
,故椭圆方程为![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: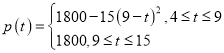 ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别为AB,AC的中点,O为DE的中点,AB=AC=2![]() ,BC=4.将△ADE沿DE折起到△A1DE的位置,使得平面A1DE
,BC=4.将△ADE沿DE折起到△A1DE的位置,使得平面A1DE![]() 平面BCED,如下图.
平面BCED,如下图.

(Ⅰ)求证:A1O![]() BD;
BD;
(Ⅱ)求直线A1C和平面A1BD所成角的正弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.
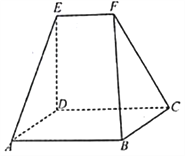
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() ,
,![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若直线![]() 的方程为
的方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为![]() ,对该款智能家电的评分为
,对该款智能家电的评分为![]() .若根据统计数据,用最小二乘法得到
.若根据统计数据,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,且年龄
,且年龄![]() 的方差为
的方差为![]() ,评分
,评分![]() 的方差为
的方差为![]() .求
.求![]() 与
与![]() 的相关系数
的相关系数![]() ,并据此判断对该款智能家电的评分与年龄的相关性强弱.
,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有![]() 的把握认为对该智能家电的评价与年龄有关.
的把握认为对该智能家电的评价与年龄有关.
好评 | 差评 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:线性回归直线![]() 的斜率
的斜率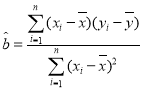 ;相关系数
;相关系数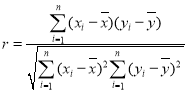 ,独立性检验中的
,独立性检验中的![]() ,其中
,其中![]() .
.
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,![]() ,
,![]() ,
,![]() ,点E是CD边的中点,将
,点E是CD边的中点,将![]() 沿AE折起,使点D到达点P的位置,且
沿AE折起,使点D到达点P的位置,且![]() .
.

(1)求证;平面![]() 平面ABCE;
平面ABCE;
(2)求点E到平面PAB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com