
(14分) 已知函数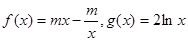 .
.
(1)当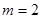 时,求曲线
时,求曲线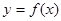 在点
在点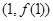 处的切线方程;
处的切线方程;
(2)当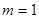 时,判断方程
时,判断方程 实根个数.
实根个数.
(3)若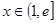 时,不等式
时,不等式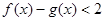 恒成立,求实数
恒成立,求实数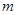 的取值范围.
的取值范围.
(1) ;(2)在
;(2)在 内
内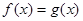 有且仅有一个实数根
有且仅有一个实数根
(3)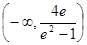
【解析】
试题分析:(1)利用导数的几何意义得到导数的值,切点坐标得到结论。
(2) 时,令
时,令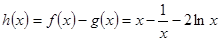 ,
,
求解导数,并判定又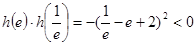 ,
,
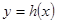 在
在 内有且仅有一个零点进而得到结论。
内有且仅有一个零点进而得到结论。
(3)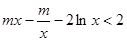 恒成立,
即
恒成立,
即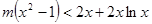 恒成立,
恒成立,
又 ,则当
,则当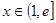 时,
时,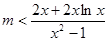 恒成立,
恒成立,
分离参数法构造新函数利用求解的最小值得到参数m的范围。
(1)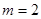 时,
时, ,
,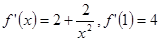 ,切点坐标为
,切点坐标为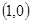 ,
,
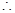 切线方程为
切线方程为
(2) 时,令
时,令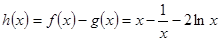 ,
,
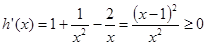 ,
,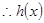 在
在 上为增函数
上为增函数
又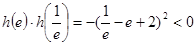 ,
,
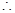
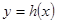 在
在 内有且仅有一个零点
内有且仅有一个零点
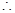 在
在 内
内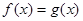 有且仅有一个实数根
有且仅有一个实数根
(或说明 也可以)
也可以)
(3)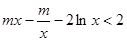 恒成立,
即
恒成立,
即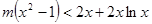 恒成立,
恒成立,
又 ,则当
,则当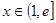 时,
时,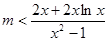 恒成立,
恒成立,
令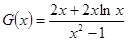 ,只需
,只需 小于
小于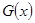 的最小值,
的最小值,
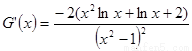 ,
,
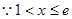 ,
, ,
,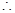 当
当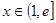 时
时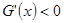 ,
,
 在
在 上单调递减,
上单调递减, 在
在 的最小值为
的最小值为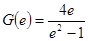 ,
,
则 的取值范围是
的取值范围是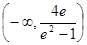
考点:本题主要是考查导数在研究函数中的运用,求解最值和导数几何意义的综合运用。
点评:解决该试题的关键是能将不等式的恒成立问题转化为哈双女户的最值来处理,并得到参数的范围,同时要理解导数的几何意义表示的为切线的斜率。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2011届北京市西城区高三二模考试理科数学 题型:解答题
((本小题满分14分)
已知函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当 时,求曲线
时,求曲线 在
在 处的切线与坐标轴围成的面积;
处的切线与坐标轴围成的面积;
(Ⅱ)若函数 存在一个极大值点和一个极小值点,且极大值与极小值的积为
存在一个极大值点和一个极小值点,且极大值与极小值的积为 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省漳州市四地七校高三第四次联考理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为 ;②
;② 是偶函数;③
是偶函数;③ 时,
时, ,其中
,其中 .
.
(Ⅰ)求 在
在 上的解析式,并求出函数
上的解析式,并求出函数 的最大值;
的最大值;
(Ⅱ)当 ,
, 时,函数
时,函数 ,若
,若 的图象恒在直线
的图象恒在直线 上方,求实数
上方,求实数 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数, ).
).
查看答案和解析>>
科目:高中数学 来源:2010年福建省高三模拟考试数学(理科)试题 题型:解答题
(本小题满分14分)
已知函数 .
.
(Ⅰ)若 为
为 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅲ)若 时,方程
时,方程 有实根,求实数
有实根,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com