
����Ŀ����֪��ԲC��![]() ��a��b��0�������ҽ���ֱ�ΪF1��F2����������Ϊ
��a��b��0�������ҽ���ֱ�ΪF1��F2����������Ϊ![]() ��MΪ��Բ������һ�㣬����F1MF2��90��ʱ����F1MF2�����Ϊ1��
��MΪ��Բ������һ�㣬����F1MF2��90��ʱ����F1MF2�����Ϊ1��
��������ԲC�ķ��̣�
������֪��A����ԲC��������Բ�����һ�㣬�ӳ�ֱ��AF1��AF2�ֱ�����Բ���ڵ�B��D����ֱ��BD��б��Ϊk1��ֱ��OA��б��Ϊk2����֤��k1��k2���ڶ�ֵ��
���𰸡�����![]() ����������
����������
��������
��������������![]() ����
����![]() ����Բ
����Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
������![]() ��
��![]() ��
��
��ֱ��![]() ��б�ʲ����ڻ�ֱ��
��б�ʲ����ڻ�ֱ��![]() ��б�ʲ�����ʱ��
��б�ʲ�����ʱ��![]() .
.
��ֱ��![]() ��
��![]() ��б�ʴ���ʱ��
��б�ʴ���ʱ��![]() ,��ֱ��
,��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ������ֱ�߷�������Բ���̣����Τ�ﶨ������ɵ�ֱ��
������ֱ�߷�������Բ���̣����Τ�ﶨ������ɵ�ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ����
����![]() .���Ͽɵã�ֱ��
.���Ͽɵã�ֱ��![]() ��
��![]() ��б��֮��Ϊ��ֵ
��б��֮��Ϊ��ֵ![]() .
.
������![]() ����
����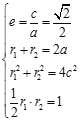 ��
��
���![]() ����
����![]() ��
��![]() ��Բ
��Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
������![]() ��
��![]() ����ֱ��
����ֱ��![]() ��б�ʲ�����ʱ��
��б�ʲ�����ʱ��
��![]() ����
����![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ����
����![]() ��
��
�ɵ�![]()
![]() ��
��![]() ����
����![]() ,
,
![]() ֱ��
ֱ��![]() ��б��Ϊ
��б��Ϊ ��ֱ��
��ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ��
��
![]() ��
��
��ֱ��![]() ��б�ʲ�����ʱ��ͬ���ɵ�
��б�ʲ�����ʱ��ͬ���ɵ�![]() .
.
��ֱ��![]() ��
��![]() ��б�ʴ���ʱ��
��б�ʴ���ʱ��![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
���� ��ȥ
��ȥ![]() �ɵã�
�ɵã�![]() ��
��
��![]() ����
����![]() �������������̿ɵ�:
�������������̿ɵ�:
![]() ��
��![]() ��
��
��![]()
![]() ��
��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��ͬ���ɵ�
��ͬ���ɵ�![]() ��
��
![]() ֱ��
ֱ��![]() ��б��Ϊ
��б��Ϊ
![]() ֱ��
ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ��
��![]()
 .
.
���ԣ�ֱ��![]() ��
��![]() ��б��֮��Ϊ��ֵ
��б��֮��Ϊ��ֵ![]() ����
����![]() .
.
���㾦��
(1)���ֱ������Բ����Ŀʱ��ʱ�����������ߵķ�����������ȥx(��y)����һԪ���η��̣�Ȼ���������ϵ���Ĺ�ϵ��������������������йزα����ĵ�����ϵ��
(2)�漰��ֱ�߷��̵��跨ʱ����ؿ���ȫ�棬��Ҫ����ֱ��б��Ϊ0���ڵ��������Σ�
�����͡������
��������
21
����Ŀ����֪����f��x������x��b����![]() ��a������b��0�����ڣ���1��f����1�����������߷���Ϊ��e��1��x��ey��e��1��0��
��a������b��0�����ڣ���1��f����1�����������߷���Ϊ��e��1��x��ey��e��1��0��
������a��b��
����������f��x����m������ʵ����x1��x2����x1��x2��֤����x2��x1��1��![]() ��
��
���𰸡�����![]() ��
��![]() ����������
����������
��������
���������������õ������о����������߷��̣��õ�����a,b�ķ����飬��ⷽ���鲢����ɵ�![]() ��
��![]() .
.
�����ɣ���֪![]() ����
����![]() ��(-1��0)�������߷���Ϊ
��(-1��0)�������߷���Ϊ![]() �����캯��
�����캯��![]() ������¹��캯�������ʷ������ۼ���֤�����еIJ���ʽ.
������¹��캯�������ʷ������ۼ���֤�����еIJ���ʽ.
����������![]() ������
������![]() ��
��
��![]() ������
������![]() ��
��
��![]() ����
����![]() ����
����![]() ì�ܣ�
ì�ܣ�
��![]() ��
��![]() .
.
�����ɣ���֪![]() ��
�� ![]() ��
��
��![]() ��(-1��0)�������߷���Ϊ
��(-1��0)�������߷���Ϊ![]() ���ã�
���ã�![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ����
ʱ����![]() ��
�� ![]() ��
��
�ʺ���![]() ��
��![]() �ϵ�����������
�ϵ�����������![]() ��
��
���Ե�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
���Ժ���![]() ������
������![]() �ϵ����ݼ���������
�ϵ����ݼ���������![]() �ϵ���������
�ϵ���������
��![]() .
.
![]() ����
����![]() �ĸ�Ϊ
�ĸ�Ϊ![]() ����
����![]() �ֺ���
�ֺ���![]() �����ݼ���
�����ݼ���
��![]() ����
����![]() ��
��
��![]() ��(0,0)�������߷���Ϊ
��(0,0)�������߷���Ϊ![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]()
�ʺ���![]() ��
��![]() �ϵ�����������
�ϵ�����������![]() ��
��
���Ե�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
���Ժ���![]() ������
������![]() �ϵ����ݼ���������
�ϵ����ݼ���������![]() �ϵ���������
�ϵ���������
![]() ��
��![]()
��![]() �ĸ�Ϊ
�ĸ�Ϊ![]() ����
����![]() �ֺ���
�ֺ���![]() ����������
����������
��![]() ����
����![]() ��
��
��![]() ��
��![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() =
= ![]() ��
�� ![]() =��sin��x��0�������Цأ�0���Ǻ���f��x��=��
=��sin��x��0�������Цأ�0���Ǻ���f��x��=�� ![]() +
+ ![]() ��
�� ![]() ��
�� ![]() ��������f��x����ͼ����ֱ��y=m��mΪ���������У������е�ĺ��������γɹ����ǦеĵȲ����У�
��������f��x����ͼ����ֱ��y=m��mΪ���������У������е�ĺ��������γɹ����ǦеĵȲ����У�
������f��x���ı���ʽ��m��ֵ��
����f��x����ͼ������ƽ�� ![]() ����λ���ٽ��õ���ͼ���ϸ�����������Ϊԭ����2���������겻�䣩��õ�y=g��x����ͼ����y=g��x����
����λ���ٽ��õ���ͼ���ϸ�����������Ϊԭ����2���������겻�䣩��õ�y=g��x����ͼ����y=g��x���� ![]() �ϵ�ֵ��
�ϵ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����4����ͬ����4����ͬ�ĺ��ӣ�����ȫ����������ڣ�
(1)���м��ַŷ���
(2)ǡ��1���պУ��м��ַŷ���
(3)ǡ��2�����Ӳ������м��ַŷ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڿռ��ı���ABCD��A��B��C��D�����棩�У�һ��ƽ�����AB��BC��CD��DA�ֱ���E��F��G��H�������˵㣩�������н��۴�����ǣ� �� 
A.��AE��BE=CF��BF����AC��ƽ��EFGH
B.��E��F��G��H�ֱ�Ϊ�����е㣬���ı���EFGHΪƽ���ı���
C.��E��F��G��H�ֱ�Ϊ�����е���AC=BD�����ı���EFGHΪ����
D.��E��F��G��H�ֱ�Ϊ�����е���AC��BD�����ı���EFGHΪ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĵ�������f��x������������x1 �� x2 �� ����f��x1+x2��=f��x1��+f��x2������������ʵ��a��b����f��a��+f��2b��1��=0���� ![]() ����СֵΪ ��
����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ ��
��![]() ��
�� ![]() Ϊ��������������ԭ��
Ϊ��������������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ��������Ϊ���Ὠ��������ϵ��ֱ��
��������Ϊ���Ὠ��������ϵ��ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ����ֱ��
����ֱ��![]() ������
������![]() ����
����
��1��������![]() �ļ����귽�̣�
�ļ����귽�̣�
��2��������![]() ��ȡ����
��ȡ����![]() ��
�� ![]() ��ԭ��
��ԭ��![]() ����
����![]() ��������
��������![]() �������
�������![]() �����ֵ.
�����ֵ.
���𰸡���1��![]() ����2��
����2��![]()
�������������������1�����ü�������ֱ������Ļ�����ʽ�ɵ�ֱ��![]() ��ֱ�����귽��Ϊ
��ֱ�����귽��Ϊ![]() ��
��
����ȥ����![]() ��֪����
��֪����![]() ��Բ��Ϊ
��Բ��Ϊ![]() ���뾶Ϊ
���뾶Ϊ![]() ��Բ����ֱ��
��Բ����ֱ��![]() ������
������![]() ���У��ɵã�
���У��ɵã� ![]() ��������C�ķ���Ϊ
��������C�ķ���Ϊ![]() �� �ٴ����ü�������ֱ������Ļ�����ʽ�ɵ�
�� �ٴ����ü�������ֱ������Ļ�����ʽ�ɵ�
�ɵ�����C�ļ����귽��.
(2)�ɣ�1��������M��![]() ����
����![]() ����
����![]() ����
����
![]() ��
��
![]() ��
��
�ɴ˿���![]() ��������ֵ.
��������ֵ.
�����������1���������ֱ֪��![]() ��ֱ�����귽��Ϊ
��ֱ�����귽��Ϊ![]() ��
��
����![]() ��Բ��Ϊ
��Բ��Ϊ![]() ���뾶Ϊ
���뾶Ϊ![]() ��Բ��ֱ��
��Բ��ֱ��![]() ������
������![]() ���У��ɵã�
���У��ɵã�  ����֪����C�ķ���Ϊ
����֪����C�ķ���Ϊ![]() ��
��
��������C�ļ����귽��Ϊ![]() ��
��
��![]() .
.
(2)�ɣ�1��������M��![]() ����
����![]() ����
����![]() ����
����
![]() ��
��

![]() ��
��
��![]() ʱ��
ʱ�� ![]() ��
��
���ԡ�MON��������ֵΪ![]() .
.
�����͡������
��������
23
����Ŀ����֪����![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ��
��
��1����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ʵ��![]() Ϊ
Ϊ![]() �����ֵ����ʵ��
�����ֵ����ʵ��![]() ��
�� ![]() ��
�� ![]() ����
����![]() ����
����![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����a=(1,sin x),b=![]() ,����f(x)=a��b-
,����f(x)=a��b-![]() cos 2x.
cos 2x.
(1)����f(x)�Ľ���ʽ���䵥����������;
(2)��x��![]() ʱ,����f(x)��ֵ��.
ʱ,����f(x)��ֵ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �Ķ�����ΪD�������ڱ�����
�Ķ�����ΪD�������ڱ�����![]() ��ʹ�ú���
��ʹ�ú���![]() ���㣺��
���㣺��![]() ��
��![]() ���ǵ�����������
���ǵ�����������![]() ��
��![]() �ϵ�ֵ��Ϊ
�ϵ�ֵ��Ϊ![]() ���������
���������![]() Ϊ
Ϊ![]() ������ֵ������.���к����д�������ֵ����������_______
������ֵ������.���к����д�������ֵ����������_______
��![]() ��
��![]() ��
��![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com