
【题目】已知曲线C1: ![]() ,(t为参数)曲线C2:
,(t为参数)曲线C2: ![]() +y2=4.
+y2=4.
(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换y′=yx,后得到曲线C′.求曲线C′的普通方程,并写出它的参数方程;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C′上的动点,求PQ中点M到直线C3:
,Q为C′上的动点,求PQ中点M到直线C3: ![]() (t为参数)的距离的最小值.
(t为参数)的距离的最小值.
【答案】
(1)解:由 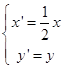 得到
得到 ![]() ①
①
将①代入曲线C2: ![]() +y2=4.得
+y2=4.得 ![]() +(y′)2=4,即(x′)2+(y′)2=4.
+(y′)2=4,即(x′)2+(y′)2=4.
因此椭圆 ![]() +y2=4经伸缩变换后得到的曲线方程是x2+y2=4.
+y2=4经伸缩变换后得到的曲线方程是x2+y2=4.
它的参数方程为 ![]()
(2)解:当t=π/2时,P(﹣4,4),Q(2cosθ,2sinθ),故M(﹣2+cosθ,2+sinθ)
曲线C3:为直线x﹣2y+8=0,
M到C3的距离d= ![]() |(﹣2+cosθ)﹣2(2+sinθ)+8|=
|(﹣2+cosθ)﹣2(2+sinθ)+8|= ![]() |cosθ﹣2sinθ+2|=
|cosθ﹣2sinθ+2|= ![]() |
| ![]() cos(θ+α)+2|
cos(θ+α)+2|
从而tanα=2时d的最小值为 ![]() |﹣
|﹣ ![]() +2|=
+2|= ![]()
【解析】(1)由 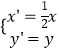 得到
得到 ![]() ,代入曲线C2:
,代入曲线C2: ![]() +y2=4.化简可得椭圆
+y2=4.化简可得椭圆 ![]() +y2=4经伸缩变换后得到的曲线方程.利用平方关系可得它的参数方程.(2)当t=
+y2=4经伸缩变换后得到的曲线方程.利用平方关系可得它的参数方程.(2)当t= ![]() 时,P(﹣4,4),Q(2cosθ,2sinθ),故M(﹣2+cosθ,2+sinθ).曲线C3:为直线x﹣2y+8=0,利用点到直线的距离公式可得M到C3的距离d=
时,P(﹣4,4),Q(2cosθ,2sinθ),故M(﹣2+cosθ,2+sinθ).曲线C3:为直线x﹣2y+8=0,利用点到直线的距离公式可得M到C3的距离d= ![]() |
| ![]() cos(θ+α)+2|,利用三角函数的单调性即可得出.
cos(θ+α)+2|,利用三角函数的单调性即可得出.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:高中数学 来源: 题型:
【题目】古希腊杰出的数学家丢番图的墓碑上有这样一首诗:
这是一座古墓,里面安葬着丢番图.
请你告诉我,丢番图的寿数几何?
他的童年占去了一生的六分之一,
接着十二分之一是少年时期,
又过了七分之一的时光,他找到了自己的终身伴侣.
五年之后,婚姻之神赐给他一个儿子,
可是儿子不济,只活到父亲寿数的一半,就匆匆离去.
这对父亲是一个沉重的打击,
整整四年,为失去爱子而悲伤,
终于告别了数学,离开了人世.
试用循环结构,写出算法分析和算法程序.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是![]() .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,周期是
,周期是![]() .
.
(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点![]() ,点
,点![]() 是该函数图象上一点,点
是该函数图象上一点,点![]() 是
是![]() 的中点,当
的中点,当![]() ,
, ![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子商务公司对10 000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
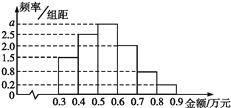
(1)直方图中的a=_____;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设X是一个离散型随机变量,则下列不能成为X的概率分布列的一组数据是( )
A.0, ![]() ,0,0,
,0,0, ![]()
B.0.1,0.2,0.3,0.4
C.p,1﹣p(0≤p≤1)
D.![]() ,
, ![]() ,…,
,…, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|1<2x<8},B={x| ![]() +1<0},C={x|a<x<a+1}.
+1<0},C={x|a<x<a+1}.
(1)求集合UA∩B;
(2)若B∪C=B,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com