
如图,在直棱柱ABC—A1B1C1中,AC=BC=2,∠ACB=90º,AA1=2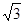 ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).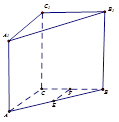
A.3或1 B.1 C.4或1 D.3或4
A
解析试题分析:根据截面与平面ABC所成的二面角的大小为60°,故需要分类讨论,利用截面为梯形,可以计算各边长,从而可求截面的面积.解:解:由题意,分类讨论:如右图,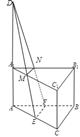
截面为MNFE,延长EM,CN,AA1,交于点D,∵直棱柱ABC-A1B1C1中,∠ACB=90°,E、F分别是AC、AB的中点,∴DE⊥EF,∴∠AED为截面与平面ABC所成的二面角,∴∠AED=60°,∵AE= AC=1,∴DE=2∵EF=
AC=1,∴DE=2∵EF=
BC=1∴S△DEF= ×2×1=1,∵DA=6
×2×1=1,∵DA=6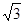 ,∴DA1=
,∴DA1= DA∴SDMN=
DA∴SDMN=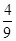 S△DEF=
S△DEF=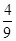 ,∴截面的面积为1
,∴截面的面积为1
设截面EFN'M'在底面中的射影为EFPQ,则EF=1,M'Q=2,CE=1,∠M'EQ=60°,∴EQ=
∴PQ=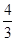 ∴射影EFPQ的面积为
∴射影EFPQ的面积为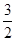 ,∵截面与平面ABC所成的二面角的大小为60°,∴截面EFN'M'的面积为
,∵截面与平面ABC所成的二面角的大小为60°,∴截面EFN'M'的面积为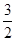 ÷cos60°=3故答案为A
÷cos60°=3故答案为A
考点:截面面积
点评:本题以直三棱柱为载体,考查截面面积的计算,搞清截面图形是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:单选题
已知长方体ABCD—A1B1ClD1内接于球O,底面ABCD是边长为2的正方形,E为AA1的中点,OA⊥平面BDE,则球O的表面积为
A.8 | B.16 : : | C.14 | D.18 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在棱长为1的正方体ABCD—A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
A.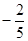 | B.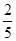 | C.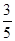 | D.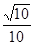 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,若
,过A、B分别作两平面交线的垂线,垂足为A′、B′,若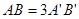 ,则AB与平面β所成的角的正弦值是( )
,则AB与平面β所成的角的正弦值是( )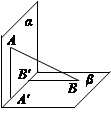
A.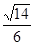 | B.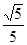 | C.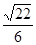 | D.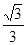 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知 是直线,
是直线, 是平面,给出下列命题:
是平面,给出下列命题:
①若 ,
, ,
, ,则
,则 或
或 .
.
②若 ,
, ,
, ,则
,则 .
.
③若m
 ,n
,n
 ,m∥
,m∥ ,n∥
,n∥ ,则
,则 ∥
∥
④若 ,
, 且
且 ,
, ,则
,则
其中正确的命题是( )。
| A.①② | B.②④ | C.②③ | D.③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D、E、F分别是棱AB、BC、CP的中点,AB=AC=1,PA=2,则直线PA与平面DEF所成角的正弦值为( )
A.  B.
B.  C.
C. 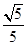 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com