
| m |
| n |
| ||
| 2 |
| m |
| n |
| 3 |
| π |
| 4 |
| m |
| n |
| ||
| 2 |
| ||||
| 2 |
| m |
| n |
| ||
| 2 |
| m |
| n |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||||
| 4 |
| asinC |
| sinA |
| 1×sin105° |
| sin30° |
| ||||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
| 2 |
| ||
| 2 |
| ||
| 4 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
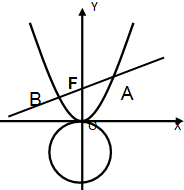 已知抛物线C:x2=4y,过焦点F的直线l与抛物线交于A,B两点(A在第一象限).
已知抛物线C:x2=4y,过焦点F的直线l与抛物线交于A,B两点(A在第一象限).| |MN| |
| d |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 组数 | 分组 | 抢购商品的人数 | 占本组的频率 |
| 第一组 | [25,30] | 120 | 0.6 |
| 第二组 | (30,35] | 195 | p |
| 第三组 | (35,40] | 100 | 0.5 |
| 第四组 | (40,45] | a | 0.4 |
| 第五组 | (45,50] | 30 | 0.3 |
| 第六组 | (50,55] | 15 | 0.3 |
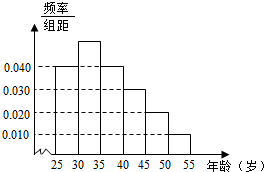
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| a |
| e1 |
| e2 |
| e1 |
| e2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| sinx |
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∧(¬q)是真命题 |
| D、命题p∨(¬q)是假命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com