
【题目】已知函数f(x)=lnx﹣ ![]() 有两个零点x1、x2 .
有两个零点x1、x2 .
(1)求k的取值范围;
(2)求证:x1+x2> ![]() .
.
【答案】
(1)解:函数f(x)=lnx﹣ ![]() 有2个零点,
有2个零点,
即函数g(x)=xlnx的图象与直线y=k有2个交点,
g′(x)=lnx+1,
令g′(x)>0,解得:x> ![]() ,令g′(x)<0,解得:0<x<
,令g′(x)<0,解得:0<x< ![]() ,
,
∴g(x)在(0, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
x= ![]() 是极小值点,g(
是极小值点,g( ![]() )=﹣
)=﹣ ![]() ,
,
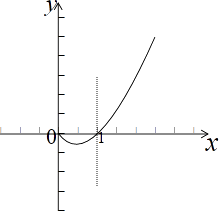
又x→0时,g(x)→0,
x→+∞时,g(x)→+∞,g(1)=0,
g(x)的大致图象如图示:
 ;
;
由图象得:﹣ ![]() <k<0
<k<0
(2)证明:不妨设x1<x2,由(1)得:0<x1< ![]() <x2<1,
<x2<1,
令h(x)=g(x)﹣g( ![]() ﹣x)=xlnx﹣(
﹣x)=xlnx﹣( ![]() ﹣x)ln(
﹣x)ln( ![]() ﹣x),
﹣x),
h′(x)=ln[﹣(ex﹣1)2+1],
当0<x< ![]() 时,h′(x)<0,h(x)在(0,
时,h′(x)<0,h(x)在(0, ![]() )递减,h(
)递减,h( ![]() )=0,
)=0,
∴h(x1)>0,即g(x1)>g( ![]() ﹣x1),g(x2)>g(
﹣x1),g(x2)>g( ![]() ﹣x1),
﹣x1),
x2, ![]() ﹣x1∈(
﹣x1∈( ![]() ,+∞),g(x)在(
,+∞),g(x)在( ![]() ,+∞)递增,
,+∞)递增,
∴x2> ![]() ﹣x1,
﹣x1,
故x1+x2> ![]()
【解析】(1)问题转化为函数g(x)=xlnx的图象与直线y=k有2个交点,求出g(x)的单调性,画出函数图象,从而求出k的范围即可;(2)设x1<x2 , 根据函数的单调性得到x2 , ![]() ﹣x1∈(
﹣x1∈( ![]() ,+∞),g(x)在(
,+∞),g(x)在( ![]() ,+∞)递增,从而证出结论即可.
,+∞)递增,从而证出结论即可.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆C以坐标轴为对称轴,以坐标原点为对称中心,椭圆的一个焦点为![]() ,点
,点![]() 在椭圆上,
在椭圆上,
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程.
求椭圆C的方程.
![]() Ⅱ
Ⅱ![]() 斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是错误命题的个数有( )
(1)若命题p为假命题,命题![]() 为假命题,则命题“
为假命题,则命题“![]() ”为假命题;
”为假命题;
(2)命题“若![]() ,则
,则![]() 或
或![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() 或
或![]() ”;
”;
(3)对立事件一定是互斥事件;
(4)![]() 为两个事件,则P(A∪B)=P(A)+P(B);
为两个事件,则P(A∪B)=P(A)+P(B);
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为正数,给出下列命题:
①若a2﹣b2=1,则a﹣b<1;
②若 ![]() ﹣
﹣ ![]() =1,则a﹣b<1;
=1,则a﹣b<1;
③ea﹣eb=1,则a﹣b<1;
④若lna﹣lnb=1,则a﹣b<1.
期中真命题的有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C:![]() 及点
及点![]() ,
,![]() .
.
![]() 过B作直线l与圆C相交于M,N两点,
过B作直线l与圆C相交于M,N两点,![]() ,求直线l的方程;
,求直线l的方程;
![]() 在圆C上是否存在点P,使得
在圆C上是否存在点P,使得![]() ?若存在,求点P的个数;若不存在,说明理由.
?若存在,求点P的个数;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生一次数学考试成绩频率分布直方图如图所示,数据分组依次为[70,90),[90,110),[110,130),[130,150],若成绩大于等于90分的人数为36,则成绩在[110,130)的人数为( ) 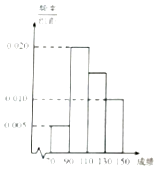
A.12
B.9
C.15
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+2=an+1﹣an , 且a1=2,a2=3,Sn为数列{an}的前n项和,则S2016的值为( )
A.0
B.2
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
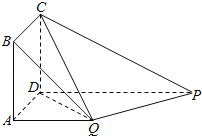
【题目】如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.
(1)证明:平面PQC⊥平面DCQ;
(2)求直线DQ与面PQC成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(1﹣ax)ln(x+1)﹣bx,其中a和b是实数,曲线y=f(x)恒与x轴相切于坐标原点.
(1)求常数b的值;
(2)当a=1时,讨论函数f(x)的单调性;
(3)当0≤x≤1时关于x的不等式f(x)≥0恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com