
【题目】如图,已知四棱锥P﹣ABCD的底面是矩形,侧面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中点,AC与BD的交点为M. 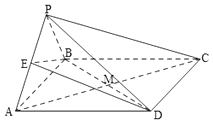
(1)求证:PC∥平面EBD;
(2)求证:BE⊥平面AED.
【答案】
(1)证明:连结EM,∵四边形ABCD是矩形,∴M为AC的中点,
∵E是PA的中点,∴EM是△PAC的中位线,
∴EM∥PC,
∵EM平面EBD,PC不包含于平面EBD,
∴PC∥平面EBD
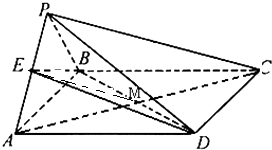
(2)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
而AD⊥AB,∴AD⊥平面PAB,
∵BE平面PAB,∴AD⊥BE,
又∵△PAB是等边三角形,且E是PA的中点,
∴BE⊥AE,
又AE∩AD=A,
∴BE⊥平面AED
【解析】(1)连结EM,由三角形中位线定理能证明PC∥平面EBD.(2)由已知条件得AD⊥平面PAB,从而得到AD⊥BE,由等边三角形性质得BE⊥AE,由此能证明BE⊥平面AED.
【考点精析】掌握直线与平面平行的判定和直线与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的通项公式为an=2n﹣1(n∈N*),且a2 , a5分别是等比数列{bn}的第二项和第三项,设数列{cn}满足cn= ![]() ,{cn}的前n项和为Sn
,{cn}的前n项和为Sn
(1)求数列{bn}的通项公式;
(2)是否存在m∈N* , 使得Sm=2017,并说明理由
(3)求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务蓬勃发展. 2016年“618”期间,某网购平台的销售业绩高达516亿元人民币,与此同时,相关管理部门推出了针对该网购平台的商品和服务的评价系统. 从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的交易为80次.
(Ⅰ) 根据已知条件完成下面的![]() 列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | |||
合计 | 200 |
(Ⅱ) 若将频率视为概率,某人在该网购平台上进行的3次购物中,设对商品和服务都满意的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附:![]()
![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn . 若对任意正整数n,总存在正整数m,使得Sn=am , 则称{an}是“H数列”.
(1)若数列{an}的前n项和Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0.若{an}是“H数列”,求d的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若对任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 的两个零点为
的两个零点为![]() ,试判断
,试判断![]() 的正负,并说明理由.
的正负,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com