
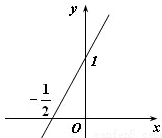
 已知二次函数f(x)=ax2+bx+c(c>0)的导函数的图象如图所示:
已知二次函数f(x)=ax2+bx+c(c>0)的导函数的图象如图所示: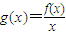 ,求y=g(x)在[1,2]上的最大值.
,求y=g(x)在[1,2]上的最大值.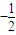 ,0)确定出一次函数解析式,求出f(x)的导函数,两者相等求出a、b即可;
,0)确定出一次函数解析式,求出f(x)的导函数,两者相等求出a、b即可;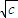 的大小范围,以[1,2]分成三个区间分别讨论,利用导数求闭区间上函数最值的方法求出最值并比较求出最大值即可;方法二:讨论x与
的大小范围,以[1,2]分成三个区间分别讨论,利用导数求闭区间上函数最值的方法求出最值并比较求出最大值即可;方法二:讨论x与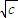 的大小利用导数求闭区间上函数最值的方法求出最值并比较求出最大值即可.
的大小利用导数求闭区间上函数最值的方法求出最值并比较求出最大值即可.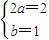 ,得
,得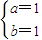 ,故所求函数解析式为f(x)=x2+x+c.
,故所求函数解析式为f(x)=x2+x+c.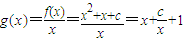 ,
,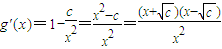 .
.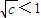 ,即0<c<1时,g′(x)>0,
,即0<c<1时,g′(x)>0,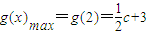 .
.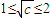 ,即1≤c≤4,当
,即1≤c≤4,当 时,g′(x)<0;当
时,g′(x)<0;当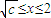 时,g′(x)>0;
时,g′(x)>0;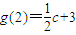 ,
, ;
;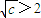 ,即c>4时,g′(x)<0,
,即c>4时,g′(x)<0,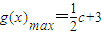 ;当c>2时,g(x)max=c+2.
;当c>2时,g(x)max=c+2.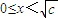 时,g′(x)<0;当
时,g′(x)<0;当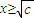 时,g′(x)>0;
时,g′(x)>0; ,
,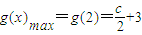 ;
;

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x) | x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com