
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定![]() 考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式
考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式![]() 随着金融业的发展,普通人能够使用的投资理财工具也多了起来
随着金融业的发展,普通人能够使用的投资理财工具也多了起来![]() 为了研究某种理财工具的使用情况,现对
为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成5组:
年龄段的人员进行了调查研究,将各年龄段人数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
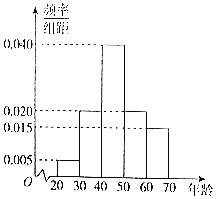
![]() Ⅰ
Ⅰ![]() 估计使用这种理财工具的人员年龄的中位数、平均数;
估计使用这种理财工具的人员年龄的中位数、平均数;
![]() Ⅱ
Ⅱ![]() 采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中各抽取多少人?
采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中各抽取多少人?
![]() Ⅲ
Ⅲ![]() 在
在![]() Ⅱ
Ⅱ![]() 中抽取的8人中,随机抽取2人,则第三组至少有1个人被抽到的概率是多少?
中抽取的8人中,随机抽取2人,则第三组至少有1个人被抽到的概率是多少?
【答案】(Ⅰ) 中位数为![]() ,平均数为47;(Ⅱ) 三个组依次抽取的人数为2,4,2;(Ⅲ)
,平均数为47;(Ⅱ) 三个组依次抽取的人数为2,4,2;(Ⅲ)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 由频率分布直方图能求出中位数和平均数的估计值;
由频率分布直方图能求出中位数和平均数的估计值;![]() Ⅱ
Ⅱ![]() 第二组、第三组、第四组的频率比为1:2:1,由此能求出三个组依次抽取的人数;
第二组、第三组、第四组的频率比为1:2:1,由此能求出三个组依次抽取的人数;![]() Ⅲ
Ⅲ![]() 在
在![]() Ⅱ
Ⅱ![]() 中抽取的8人中,随机抽取2人,基本事件总数
中抽取的8人中,随机抽取2人,基本事件总数![]() ,第三组至少有1个人被抽到的对立事件是第三组没有人被抽到,利用对立事件概率计算公式能求出第三组至少有1个人被抽到的概率.
,第三组至少有1个人被抽到的对立事件是第三组没有人被抽到,利用对立事件概率计算公式能求出第三组至少有1个人被抽到的概率.
![]() Ⅰ
Ⅰ![]() 年龄在
年龄在![]() ,
,![]() ,
,![]() 的频率为
的频率为![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 中位数为
中位数为![]() ,
,
平均数的估计值为:![]() .
.
![]() Ⅱ
Ⅱ![]() 第二组、第三组、第四组的频率比为1:2:1,
第二组、第三组、第四组的频率比为1:2:1,
![]() 三个组依次抽取的人数为2,4,2.
三个组依次抽取的人数为2,4,2.
![]() Ⅲ
Ⅲ![]() 在
在![]() Ⅱ
Ⅱ![]() 中抽取的8人中,随机抽取2人,
中抽取的8人中,随机抽取2人,
基本事件总数![]() ,
,
第三组至少有1个人被抽到的对立事件是第三组没有人被抽到,
![]() 第三组至少有1个人被抽到的概率
第三组至少有1个人被抽到的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】某校从高一年级参加期末考试的学生中抽出50名学生,并统计了他们的数学成绩(满分为100分),将数学成绩进行分组,并根据各组人数制成如下频率分布表:

(1)写出![]() 的值,并估计本次考试全年级学生的数学平均分(同一组中的数据用该组区间的中点值作代表);
的值,并估计本次考试全年级学生的数学平均分(同一组中的数据用该组区间的中点值作代表);
(2)现从成绩在![]() 内的学生中任选出两名同学,从成绩在
内的学生中任选出两名同学,从成绩在![]() 内的学生中任选一名同学,共三名同学参加学习习惯问卷调查活动.若
内的学生中任选一名同学,共三名同学参加学习习惯问卷调查活动.若![]() 同学的数学成绩为43分,
同学的数学成绩为43分,![]() 同学的数学成绩为
同学的数学成绩为![]() 分,求
分,求![]() 两同学恰好都被选出的概率.
两同学恰好都被选出的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程(2+λ)x-(1+λ)y-2(3+2λ)=0与点P(-2,2).
(1)证明:对任意的实数λ,该方程都表示直线,且这些直线都经过同一定点,并求出这一定点的坐标;
(2)证明:该方程表示的直线与点P的距离d小于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),
是参数),
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 任一点为
任一点为![]() ,求点
,求点![]() 直线
直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·开封二模)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率.
(2)检验结束后,甲、乙两名运动员的成绩用茎叶图表示如图:
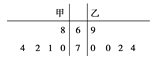
计算说明哪位运动员的成绩更稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校某班在一次数学测验中,全班N名学生的数学成绩的频率分布直方图如下,已知分数在110~120的学生有14人.

(1)求总人数N和分数在120~125的人数n;
(2)利用频率分布直方图,估算该班学生数学成绩的众数和中位数各是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:①若
有下述四个结论:①若![]() ,则
,则![]() ;②
;②![]() 的图象关于点
的图象关于点![]() 对称;③函数
对称;③函数![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的图象向右平移
的图象向右平移![]() 个单位长度后所得图象关于
个单位长度后所得图象关于![]() 轴对称.其中所有正确结论的编号是( )
轴对称.其中所有正确结论的编号是( )
A.①②④B.①②C.③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于![]() 到
到![]() 之间,将数据分成以下
之间,将数据分成以下![]() 组:第
组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第
,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第![]() ,
, ![]() ,
, ![]() 组中随机抽取
组中随机抽取![]() 名学生做初检.
名学生做初检.
(![]() )求每组抽取的学生人数.
)求每组抽取的学生人数.
(![]() )若从
)若从![]() 名学生中再次随机抽取
名学生中再次随机抽取![]() 名学生进行复检,求这
名学生进行复检,求这![]() 名学生不在同一组的概率.
名学生不在同一组的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com