
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )
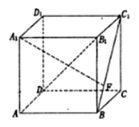
A.无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
B.当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 相交于一点,记为点
相交于一点,记为点![]() ,且
,且![]()
C.无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
D.当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
【答案】ABC
【解析】
对于A,直接证明![]() 面
面![]() 即可判断A;对于B,设A1F和B1D相交于点E,则
即可判断A;对于B,设A1F和B1D相交于点E,则![]() ,所以
,所以![]() ,即可判断B;对于C,F为BC1中点时,最小角的正切值为
,即可判断B;对于C,F为BC1中点时,最小角的正切值为![]() ,最小角大于
,最小角大于![]() ,即可判断C;对于D,当F为BC1中点时,最大角的余弦值为
,即可判断C;对于D,当F为BC1中点时,最大角的余弦值为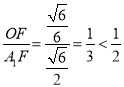 ,最大角大于
,最大角大于![]() ,可判断D.
,可判断D.
对于A选项,在正方体中,易知![]() ,由
,由![]() 面
面![]() 得
得![]() ,
,
而![]() ,故
,故![]() 面
面![]() ,所以
,所以![]() ,
,
同理可得:![]() ,
,
又因为![]() ,所以
,所以![]() 面
面![]() ,
,
又![]() 面
面![]() ,∴
,∴![]() ,即A正确;
,即A正确;
对于B选项,当点F为BC1中点时,也是B1C的中点,它们共面于平面![]() ,且必相交,设交点为E,连接A1D和B1F,如图所示:
,且必相交,设交点为E,连接A1D和B1F,如图所示:

因为![]() ,所以
,所以![]() ,故B正确;
,故B正确;
对于C选项,当F从B移至C1时,异面直线A1F与CD所成角由大变小再变大,且F为BC1中点时,最小角的正切值为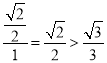 ,最小角大于
,最小角大于![]() ,即C正确;
,即C正确;
对于D选项,当点F在BC1上移动时,直线A1F与平面BDC1所成角由小变大再变小,如图所示,其中点O为A1在平面BDC1上的投影,
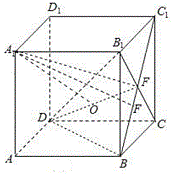
当F为BC1中点时,最大角的余弦值为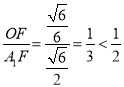 ,最大角大于
,最大角大于![]() ,故D错误,
,故D错误,
故选:ABC.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某精密仪器生产车间每天生产![]() 个零件,质检员小张每天都会随机地从中抽取50个零件进行检查是否合格,若较多零件不合格,则需对其余所有零件进行检查.根据多年的生产数据和经验,这些零件的长度服从正态分布
个零件,质检员小张每天都会随机地从中抽取50个零件进行检查是否合格,若较多零件不合格,则需对其余所有零件进行检查.根据多年的生产数据和经验,这些零件的长度服从正态分布![]() (单位:微米
(单位:微米![]() ),且相互独立.若零件的长度
),且相互独立.若零件的长度![]() 满足
满足![]() ,则认为该零件是合格的,否则该零件不合格.
,则认为该零件是合格的,否则该零件不合格.
(1)假设某一天小张抽查出不合格的零件数为![]() ,求
,求![]() 及
及![]() 的数学期望
的数学期望![]() ;
;
(2)小张某天恰好从50个零件中检查出2个不合格的零件,若以此频率作为当天生产零件的不合格率.已知检查一个零件的成本为10元,而每个不合格零件流入市场带来的损失为260元.假设![]() 充分大,为了使损失尽量小,小张是否需要检查其余所有零件,试说明理由.
充分大,为了使损失尽量小,小张是否需要检查其余所有零件,试说明理由.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.
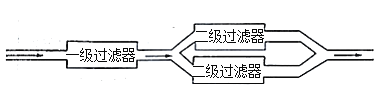
其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图
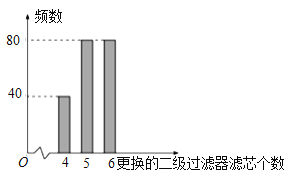
以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com