
【题目】三个数a、b、c∈(0, ![]() ),且cosa=a,sin(cosb)=b,cos(sinc)=c,则a、b、c从小到大的顺序是 .
),且cosa=a,sin(cosb)=b,cos(sinc)=c,则a、b、c从小到大的顺序是 .
【答案】b<a<c
【解析】解:先证明当x∈(0, ![]() )时,sinx<x 设y=sinx﹣x,则y′=cosx﹣1<0,∴y=sinx﹣x为(0,
)时,sinx<x 设y=sinx﹣x,则y′=cosx﹣1<0,∴y=sinx﹣x为(0, ![]() )上的减函数,∴y<sino﹣0=0,即sinx<x
)上的减函数,∴y<sino﹣0=0,即sinx<x
同理可证明f(x)=sin(cosx)﹣x为(0, ![]() )上的减函数,g(x)=cos(sinx)﹣x为(0,
)上的减函数,g(x)=cos(sinx)﹣x为(0, ![]() )上的减函数
)上的减函数
∵sina<a
∴cos(sina)﹣a=cos(sina)﹣cosa>0,而cos(sinc)﹣c=0,
∴g(a)>g(c),a、c∈(0, ![]() ),
),
∴a<c
同理∵x∈(0, ![]() )时,sinx<x,∴sin(cosa)<cosa
)时,sinx<x,∴sin(cosa)<cosa
∴sin(cosa)﹣a=sin(cosa)﹣cosa<0,而sin(cosb)﹣b=0
∴f(a)<f(b),a、b∈(0, ![]() ),
),
∴a>b
综上所述,b<a<c
所以答案是b<a<c


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,满足x2+y2≤1,x≥0,y≥0的点P(x,y)的集合对应的平面图形的面积为 ![]() ;类似的,在空间直角坐标系O﹣xyz中,满足x2+y2+z2≤1,x≥0,y≥0,z≥0的点P(x,y,z)的集合对应的空间几何体的体积为( )
;类似的,在空间直角坐标系O﹣xyz中,满足x2+y2+z2≤1,x≥0,y≥0,z≥0的点P(x,y,z)的集合对应的空间几何体的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 是奇函数,f(x)=lg(10x+1)+bx是偶函数.
是奇函数,f(x)=lg(10x+1)+bx是偶函数.
(1)求a和b的值.
(2)说明函数g(x)的单调性;若对任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求实数k的取值范围.
(3)设 ![]() ,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
分 组 | 频 数 | 频 率 |
[0,10) | 0.05 | |
[10,20) | 0.10 | |
[20,30) | 30 | |
[30,40) | 0.25 | |
[40,50) | 0.15 | |
[50,60] | 15 | |
合 计 | n | 1 |

(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:sin230°+sin290°+sin2150°= ![]() ;
;
sin25°+sin265°+sin2125°= ![]() ;
;
sin212°+sin272°+sin2132°= ![]() ;
;
通过观察上述两等式的规律,请你写出一般性的命题,并给予的证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.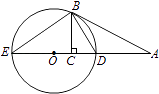
(1)证明:∠CBD=∠DBA;
(2)若AD=3DC,BC= ![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com