
【题目】已知U=R且A={x|a2x2-5ax-6<0},B{x||x-2|≥1}.
(1)若a=1,求(UA)![]() B;
B;
(2)求不等式a2x2-5ax-6<0(a∈R)的解集.
【答案】(1){x|x≤-1或x≥6};(2)a=0时,不等式的解集为R;a>0时,不等式的解集为(-![]() ,
,![]() );a<0时,不等式的解集为(
);a<0时,不等式的解集为(![]() ,-
,-![]() ).
).
【解析】
(1)解不等式求出集合![]() ,
,![]() ,再由集合运算法则计算.
,再由集合运算法则计算.
(2)分类讨论,![]() ,
,![]() 时,方程
时,方程![]() 两根为
两根为![]() 和
和![]() ,按它们的大小分类得解集.
,按它们的大小分类得解集.
(1)a=1时,A={x|x2-5x-6<0}={x|-1<x<6},B={x||x-2|≥1}={x|x≤1或x≥3};
∴UA={x|x≤-1或x≥6},
则(UA)![]() B={x|x≤-1或x≥6};
B={x|x≤-1或x≥6};
(2)a=0时,不等式化为-6<0,解集为R;
当a≠0时,不等式化为(ax+1)(ax-6)<0,即(x+![]() )(x-
)(x-![]() )<0;
)<0;
若a>0,则-![]() <
<![]() ,不等式的解集为(-
,不等式的解集为(-![]() ,
,![]() );
);
若a<0,则-![]() >
>![]() ,不等式的解集为(
,不等式的解集为(![]() ,-
,-![]() );
);
综上知,a=0时,不等式的解集为R;
a>0时,不等式的解集为(-![]() ,
,![]() );
);
a<0时,不等式的解集为(![]() ,-
,-![]() ).
).


科目:高中数学 来源: 题型:
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的![]() 城市和交通拥堵严重的
城市和交通拥堵严重的![]() 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:

(1)根据茎叶图,比较两城市满意度评分的平均值的大小(不要求计算具体值,给出结论即可);
(2)若得分不低于85分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此列联表,并据此样本分析是否有![]() 的把握认为城市拥堵与认可共享单车有关;
的把握认为城市拥堵与认可共享单车有关;
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
(3)若此样本中的![]() 城市和
城市和![]() 城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自
城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自![]() 城市的概率是多少?
城市的概率是多少?
(参考公式: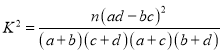 )
)
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.乘坐高铁可以网络购票,为了研究网络购票人群的年龄分布情况,在5月31日重庆到成都高铁9600名网络购票的乘客中随机抽取了120人进行了统计并记录,按年龄段将数据分成6组:![]() ,得到如下直方图:
,得到如下直方图:
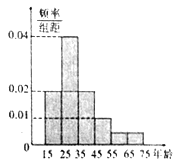
(1)试通过直方图,估计5月31日当天网络购票的9600名乘客年龄的中位数;
(2)若在调查的且年龄在![]() 段乘客中随机抽取两人,求两人均来自同一年龄段的概率.
段乘客中随机抽取两人,求两人均来自同一年龄段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
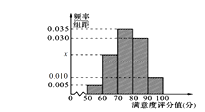
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,且该圆经过点
,且该圆经过点![]() .
.
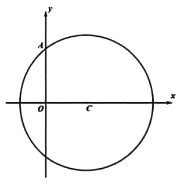
(1)求圆![]() 的标准方程;
的标准方程;
(2)若点![]() 也在圆
也在圆![]() 上,且弦
上,且弦![]() 长为8,求直线
长为8,求直线![]() 的方程;
的方程;
(3)直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,若直线
两点,若直线![]() ,
,![]() 的斜率之积为2,求证:直线
的斜率之积为2,求证:直线![]() 过一个定点,并求出该定点坐标.
过一个定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
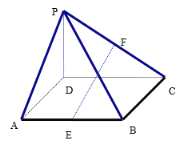
(1)求证:AB⊥平面PAD;
(2)求证:EF//平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com