
 ,函数
,函数 .
. 时,
时, ,求函数
,求函数 的单调区间;
的单调区间; 的不等式
的不等式 在区间
在区间 上有解,求
上有解,求 的取值范围;
的取值范围; 在其图象上的两点
在其图象上的两点 ,
, (
(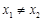 )处的切线分别为
)处的切线分别为 .若直线
.若直线 与
与 平行,试探究点
平行,试探究点 与点
与点 的关系,并证明你的结论.
的关系,并证明你的结论.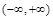 ,
, 的取值范围是
的取值范围是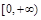 ;(2)见解析.
;(2)见解析.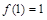 ,所以
,所以 ,得到解析式,然后分析函数的单调区间,运用导数的正负来判定即可
,得到解析式,然后分析函数的单调区间,运用导数的正负来判定即可 的不等式
的不等式 在区间
在区间 上有解,等价转化为
上有解,等价转化为 在区间
在区间 上有解,然后利用分离参数m的思想得到取值范围
上有解,然后利用分离参数m的思想得到取值范围 的对称中心为
的对称中心为 ,
, 可以由
可以由 经平移得到,
经平移得到, 的对称中心为
的对称中心为 ,故合情猜测,若直线
,故合情猜测,若直线 与
与 平行,则点
平行,则点 与点
与点 关于点
关于点 对称.然后加以证明即可。
对称.然后加以证明即可。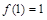 ,所以
,所以 , ……………………1分
, ……………………1分 , 而
, 而 恒成立,
恒成立,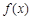 的单调递增区间为
的单调递增区间为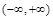 . ……………………4分
. ……………………4分 在区间
在区间 上有解,
上有解, 在区间
在区间 上有解,
上有解, 在区间
在区间 上有解,
上有解, 不小于
不小于 在区间
在区间 上的最小值. ……………………6分
上的最小值. ……………………6分 时,
时, ,
, 的取值范围是
的取值范围是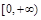 . ……………………9分
. ……………………9分 的对称中心为
的对称中心为 ,
, 可以由
可以由 经平移得到,
经平移得到, 的对称中心为
的对称中心为 ,故合情猜测,若直线
,故合情猜测,若直线 与
与 平行,则点
平行,则点 与点
与点 关于点
关于点 对称. ……………………10分
对称. ……………………10分 ,
, ,
, ,
, 的斜率分别为
的斜率分别为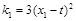 ,
, .
. 与
与 平行,所以
平行,所以 ,即
,即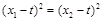 ,
,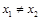 ,
, , ……………………12分
, ……………………12分 ,
, .
.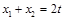 ,
, ,
, (
(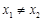 )关于点
)关于点 对称.
对称. 与
与 平行时,点
平行时,点 与点
与点 关于点
关于点 对称. ……………………14分
对称. ……………………14分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com