
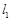 :
: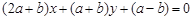 与直线
与直线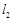 :
: .
. 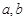 变化时,求证:直线
变化时,求证:直线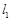 过定点,并求出这个定点的坐标;
过定点,并求出这个定点的坐标;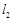 通过直线
通过直线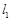 的定点,求点
的定点,求点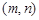 所在曲线
所在曲线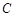 的方程;
的方程;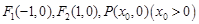 ,过点
,过点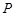 的直线交曲线
的直线交曲线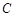 于
于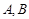 两点(
两点(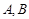 两点都在
两点都在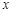 轴上方),且
轴上方),且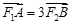 ,求此直线的方程.
,求此直线的方程.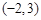 .(2)
.(2)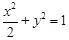 .(3)
.(3)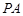 的方程为
的方程为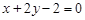 .
.  :
: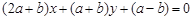 与直线
与直线 :
: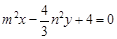 .
. 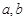 变化时,直线
变化时,直线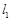 表示为过两条直线交点的直线系方程可知其过定点,并求出这个定点的坐标;
表示为过两条直线交点的直线系方程可知其过定点,并求出这个定点的坐标;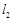 通过直线
通过直线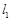 的定点,则可知点
的定点,则可知点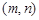 所在曲线
所在曲线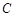 的方程;
的方程;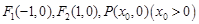 ,过点
,过点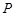 的直线交曲线
的直线交曲线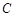 于
于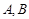 两点(
两点(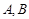 两点都在
两点都在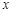 轴上方),且
轴上方),且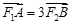 ,运用向量的共线的知识得到结论。
,运用向量的共线的知识得到结论。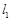 的方程化为
的方程化为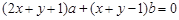 ,…………………………2分
,…………………………2分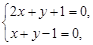 解得
解得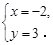 所以定点的坐标为
所以定点的坐标为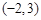 .………………4分
.………………4分 过定点
过定点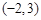 ,得
,得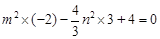 ,化简得
,化简得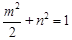 ,
,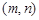 所在曲线
所在曲线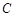 的方程为
的方程为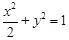 .……………………………………8分
.……………………………………8分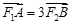 ,所以
,所以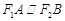 ,且
,且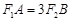 ,
, ,所以
,所以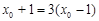 ,所以
,所以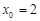 ,所以
,所以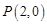 .…………10分
.…………10分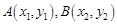 ,则
,则 ,
,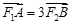 ,得
,得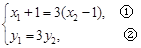 ,又由
,又由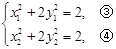
 所以
所以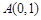 ,……………………………………………14分
,……………………………………………14分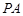 的方程为
的方程为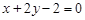 .……………………………………………………16分
.……………………………………………………16分

 全能测控期末小状元系列答案
全能测控期末小状元系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com