
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 充分而不必要条件 |
分析 根据充分条件和必要条件的定义结合函数周期性和奇偶性和单调性之间的关系进行判断即可.
解答 解:∵f(x)是定义在R上的偶函数,且以2为周期,则“f(x)在[0,1]上递增,
∴f(x)在[-1,0]上递递减,
则f(x)在[1,2]上递减,
反之若f(x)在[1,2]上递减,
∵函数f(x)是周期为2的周期函数,
∴f(x)在[-1,0]上递递减,
∵f(x)是偶函数,
∴f(x)在[0,1]上递增,
即“f(x)在[0,1]上递增”是“f(x)在[1,2]上递减”的充要条件,
故选:B.
点评 本题主要考查充分条件和必要条件的判断,根据函数奇偶性和周期性与单调性之间的关系是解决本题的关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | -4 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
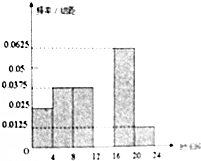 上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:
上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com