
定义在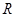 上的函数
上的函数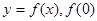
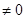 ,当
,当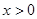 时,
时,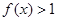 ,且对任意的
,且对任意的 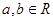 ,有
,有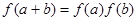 ,
,
(Ⅰ)求证: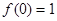 ;
;
(Ⅱ)求证:对任意的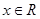 ,恒有
,恒有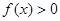 ;
;
(Ⅲ)证明: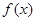 是
是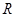 上的增函数.
上的增函数.
(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)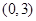 .
.
解析试题分析:(Ⅰ)令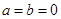 即可得证;(Ⅱ)令
即可得证;(Ⅱ)令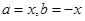 得,
得,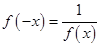 ,由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0,故对任意x∈R,f(x)>0;(Ⅲ)先证明
,由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0,故对任意x∈R,f(x)>0;(Ⅲ)先证明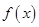 为增函数:任取x2>x1,则
为增函数:任取x2>x1,则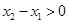 ,
,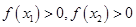 ,故
,故 ,故其为增函数.
,故其为增函数.
试题解析:(Ⅰ)令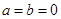 ,则f(0)=[f(0)]2 ∵ f(0)≠0 ∴ f(0)=1 2分
,则f(0)=[f(0)]2 ∵ f(0)≠0 ∴ f(0)=1 2分
(Ⅱ)令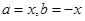 则 f(0)=f(x)f(-x)∴
则 f(0)=f(x)f(-x)∴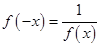 4分
4分
由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0
∴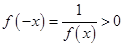 ,又x=0时,f(0)=1>0 6分
,又x=0时,f(0)=1>0 6分
∴对任意x∈R,f(x)>0 7分
(Ⅲ)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0 8分
∴
∴ f(x2)>f(x1) ∴ f(x)在R上是增函数 13分
考点:抽象函数、增函数的证明、一元二次不等式解法.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
相关部门对跳水运动员进行达标定级考核,动作自选,并规定完成动作成绩在八分及以上的定为达标,成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
(1)考核结束后,从参加考核的运动员中随机抽取了8人,发现这8人中有2人没有达标,有3人为一级运动员,据此请估计此次考核的达标率及被定为一级运动员的人数;
(2)经过考核,决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛(这五位运动员每位被选中的可能性相同). 写出所有可能情况,并求运动员E被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数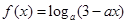 .
.
(1) 当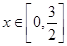 时,函数
时,函数 恒有意义,求实数a的取值范围;
恒有意义,求实数a的取值范围;
(2) 是否存在这样的实数a,使得函数 在区间
在区间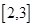 上为增函数,并且
上为增函数,并且 的最大值为1.如果存在,试求出a的值;如果不存在,请说明理由.
的最大值为1.如果存在,试求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
工厂生产某种产品,次品率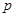 与日产量
与日产量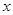 (万件)间的关系
(万件)间的关系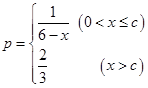 (
( 为常数,且
为常数,且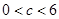 ),已知每生产一件合格产品盈利
),已知每生产一件合格产品盈利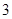 元,每出现一件次品亏损
元,每出现一件次品亏损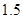 元.
元.
(1)将日盈利额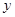 (万元)表示为日产量
(万元)表示为日产量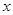 (万件)的函数;
(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?(注:  )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
二次函数f(x)满足f (x+1)-f (x)=2x且f (0)=1.
⑴求f (x)的解析式;
⑵在区间[-1,1]上,y=f (x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一家公司生产某种产品的年固定成本为10万元,每生产1千件该产品需另投入2.7万元,设该公司一年内生产该产品 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为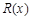 万元,且
万元,且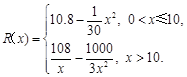
(Ⅰ)写出年利润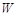 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一产品的产销过程中所获利润最大
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm;图2是双层中空玻璃,厚度均为4 mm,中间留有厚度为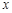 的空气隔层.根据热传导知识,对于厚度为
的空气隔层.根据热传导知识,对于厚度为 的均匀介质,两侧的温度差为
的均匀介质,两侧的温度差为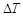 ,单位时间内,在单位面积上通过的热量
,单位时间内,在单位面积上通过的热量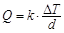 ,其中
,其中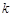 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为
为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为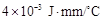 ,空气的热传导系数为
,空气的热传导系数为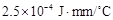 .)
.)
(1)设室内,室外温度均分别为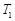 ,
,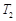 ,内层玻璃外侧温度为
,内层玻璃外侧温度为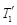 ,外层玻璃内侧温度为
,外层玻璃内侧温度为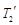 ,且
,且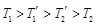 .试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用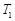 ,
,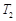 及
及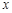 表示);
表示);
(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计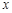 的大小?
的大小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com