
【题目】已知函数![]() 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.
(1)求![]() 的取值范围;
的取值范围;
(2)设两个极值点分别为![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)函数![]() 在其定义域内有两个不同的极值点等价于方程
在其定义域内有两个不同的极值点等价于方程![]() 在
在![]() 有两个不同根,即函数
有两个不同根,即函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,讨论函数
上有两个不同交点,讨论函数![]() 单调性和极值根据图象即可求
单调性和极值根据图象即可求![]() 的取值范围;(2)作差得,
的取值范围;(2)作差得, ![]() ,即
,即 .原不等式
.原不等式![]() 等价于
等价于![]()
![]()
![]() ,
, ![]() ,则
,则![]() ,只需证明不等式
,只需证明不等式![]() 成立即可.
成立即可.
试题解析:(1)依题意,函数![]() 的定义域为
的定义域为![]() ,所以方程
,所以方程![]() 在
在![]() 有两个不同根.
有两个不同根.
即,方程![]() 在
在![]() 有两个不同根.
有两个不同根.
转化为,函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点.
上有两个不同交点.
又![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上单调增,在
上单调增,在![]() 上单调减,从而
上单调减,从而![]() .
.
又![]() 有且只有一个零点是1,且在
有且只有一个零点是1,且在![]() 时,
时, ![]() ,在
,在![]() 时,
时, ![]() ,
,
所以![]() 的草图如下,
的草图如下,
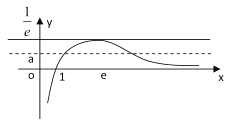
可见,要想函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,只需
上有两个不同交点,只需![]() .
.
(2)由(1)可知![]() 分别是方程
分别是方程![]() 的两个根,即
的两个根,即![]() ,
, ![]() ,
,
设![]() ,作差得,
,作差得, ![]() ,即
,即 .
.
原不等式![]() 等价于
等价于
![]()
![]()
![]()
令![]() ,则
,则![]() ,
, ![]() ,
,
设![]() ,
, ![]() ,
,  ,
,
∴函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
即不等式![]() 成立,
成立,
故所证不等式![]() 成立.
成立.


科目:高中数学 来源: 题型:
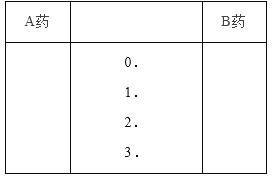
【题目】为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:

服用B药的20位患者日平均增加的睡眠时间:

(Ⅰ)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某小区准备将一块闲置的直角三角形(其中![]() )土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道
)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道![]() ,且两边是两个关于走道
,且两边是两个关于走道![]() 对称的三角形(
对称的三角形(![]() 和
和![]() ),现考虑方便和绿地最大化原则,要求
),现考虑方便和绿地最大化原则,要求![]() 点与
点与![]() 点不重合,
点不重合,![]() 点落在边
点落在边![]() 上,设
上,设![]() .
.
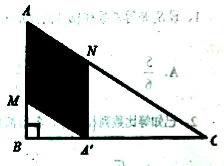
(1)若![]() ,绿地“最美”,求最美绿地的面积;
,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民行走,设计时要求![]() 最短,求此时公共绿地走道
最短,求此时公共绿地走道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将甲、乙、丙、丁四名同学按一定顺序排成一行,要求自左向右,且甲不排在第一,乙不排在第二,丙不排在第三,丁不排在第四,比如:“乙甲丁丙”是满足要求的一种排法,试写出他们四个人所有不同的排法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级学生身体素质体能测试的成绩(百分制)分布在![]() 内,同时为了了解学生爱好数学的情况,从中随机抽取了
内,同时为了了解学生爱好数学的情况,从中随机抽取了![]() 名学生,这
名学生,这![]() 名学生体能测试成绩的频率分布直方图如图所示,各分数段的“爱好数学”的人数情况如表所示.
名学生体能测试成绩的频率分布直方图如图所示,各分数段的“爱好数学”的人数情况如表所示.
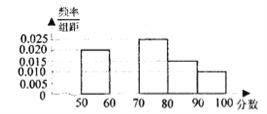
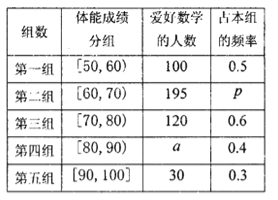
(1)求![]() 的值;
的值;
(2)用分层抽样的方法,从体能成绩在![]() 的“爱好数学”学生中随机抽取6人参加某项活动,现从6人中随机选取2人担任领队,记体能成绩在
的“爱好数学”学生中随机抽取6人参加某项活动,现从6人中随机选取2人担任领队,记体能成绩在![]() 内领队人数为
内领队人数为![]() 人,求
人,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在如下图象中的两条线段上.该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:

(1)根据提供的图象,写出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com