[题目]如图所示.直四棱柱ABCD﹣A1B1C1D1内接于半径为的半球O.四边形ABCD为正方形.则该四棱柱的体积最大时.AB的长是( ) A.1B.C.D.2 题目和参考答案——青夏教育精英家教网—

【题目】如图所示，直四棱柱ABCD﹣A1B1C1D1内接于半径为的半球O，四边形ABCD为正方形，则该四棱柱的体积最大时，AB的长是（）
A.1
B.
C.
D.2

【答案】D
【解析】解：设AB=a，BB1=h，则OB= a，连接OB1 ， OB，则OB2+BB12=OB12=3，
∴ =3，
∴a2=6﹣2h2 ，
故正四棱柱的体积是V=a2h=6h﹣2h3 ，
∴V′=6﹣6h2 ，
当0＜h＜1时，V′＞0，1＜h＜时，V′＜0，
∴h=1时，该四棱柱的体积最大，此时AB=2．
故选：D．

设AB=a，BB1=h，求出a2=6﹣2h2 ，故正四棱柱的体积是V=a2h=6h﹣2h3 ，利用导数，得到该正四棱柱体积的最大值，即可得出结论．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知，为不共共线的非零向量，且| |=| |=1，则以下四个向量中模最大者为（）
A. +
B. +
C. +
D. +

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某高职院校进行自主招生文化素质考试，考试内容为语文、数学、英语三科，总分为200分.现从上线的考生中随机抽取20人，将其成绩用茎叶图记录如下：
td style="width:16.2pt; padding:3.75pt 5.4pt; vertical-align:middle">

男				女
			15	6
	5	4	16	3	5	8
	8	2	17	2	3	6	8	8	8
	6	5	18	5	7
		19	2	3

（Ⅰ）计算上线考生中抽取的男生成绩的方差；（结果精确到小数点后一位）

（Ⅱ）从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会，求所选考生恰为一男一女的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在三棱柱中，平面平面，，，，，为的中点．

（1）求证：平面；

（2）求二面角的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．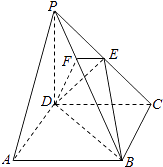
（1）证明PA∥平面EDB；
（2）证明PB⊥平面EFD；
（3）求二面角C﹣PB﹣D的大小．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知圆：和抛物线：，为坐标原点．

（1）已知直线和圆相切，与抛物线交于两点，且满足，求直线的方程；

（2）过抛物线上一点作两直线和圆相切，且分别交抛物线于两点，若直线的斜率为，求点的坐标．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】六个面都是平行四边形的四棱柱称为平行六面体．已知在平行四边形ABCD中（如图1），有AC2+BD2=2（AB2+AD2），则在平行六面体ABCD﹣A1B1C1D1中（如图2），AC12+BD12+CA12+DB12等于（）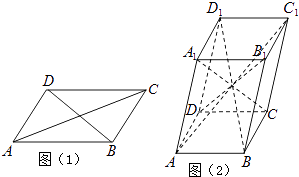
A.2（AB2+AD2+AA12）
B.3（AB2+AD2+AA12）
C.4（AB2+AD2+AA12）
D.4（AB2+AD2）