
【题目】已知函数![]() .
.
(1)当![]() 时,证明函数
时,证明函数![]() 在
在![]() 是单调函数;
是单调函数;
(2)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,
,![]() 是函数
是函数![]() 图象上任意不同的两点,记线段
图象上任意不同的两点,记线段![]() 的中点的横坐标是
的中点的横坐标是![]() ,证明直线
,证明直线![]() 的斜率
的斜率![]()
![]() .
.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:
(1)首先求解导函数,由![]() 可得函数
可得函数![]() 在
在![]() 是单增函数;
是单增函数;
(2)利用函数的单调性结合题意得到关于实数a的方程,解方程可得![]() .
.
(3)首先求得斜率的表达式,然后结合表达式设![]() ,构造新函数
,构造新函数![]() ,结合函数的特征即可证得结论.
,结合函数的特征即可证得结论.
试题解析:
(1)解:![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() .∴函数
.∴函数![]() 在
在![]() 是单增函数;
是单增函数;
(2)解:在![]() 上,分如下情况讨论:
上,分如下情况讨论:
1.当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,其最小值为
单调递增,其最小值为![]() ,这与函数在
,这与函数在![]() 上的最小值是
上的最小值是![]() 相矛盾;
相矛盾;
2.当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,其最小值为
单调递增,其最小值为![]() ,同样与最小值是相矛盾;
,同样与最小值是相矛盾;
3.当![]() 时,函数
时,函数![]() 在
在![]() 上有
上有![]() ,单调递减,在
,单调递减,在![]() 上有
上有![]() ,单调递增,
,单调递增,
∴函数![]() 的最小值为
的最小值为![]() ,得
,得![]() .
.
(3)证明:当![]() 时,
时,![]() ,
,![]() .
.
又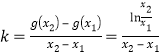 ,不妨设
,不妨设![]() ,
,
要比较![]() 与
与![]() 的大小,即比较
的大小,即比较![]() 与
与![]() 的大小,又因为
的大小,又因为![]() ,
,
所以即比较![]() 与
与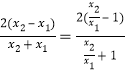 的大小.
的大小.
令![]() ,则
,则![]() ∴
∴![]() 在
在![]() 上是增函数.
上是增函数.
又![]() ,∴
,∴![]() ,
,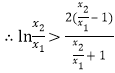 ,即
,即![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某品牌手机销售商今年1,2,3月份的销售量分别是1万部,1.2万部,1.3万部,为估计以后每个月的销售量,以这三个月的销售为依据,用一个函数模拟该品牌手机的销售量y(单位:万部)与月份x之间的关系,现从二次函数![]() 或函数
或函数![]() 中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时, ![]() ;
;
(1)求函数![]() 在
在![]() 上的解析式并画出函数
上的解析式并画出函数![]() 的图象(不要求列表描点,只要求画出草图)
的图象(不要求列表描点,只要求画出草图)
(2)(ⅰ)写出函数![]() 的单调递增区间;
的单调递增区间;
(ⅱ)若方程![]() 在
在![]() 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 与
与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() ,点
,点![]() 为椭圆的焦点,且
为椭圆的焦点,且![]() 是边长为2的等边三角形,若直线
是边长为2的等边三角形,若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
(1)直线![]() 的斜率之积是否为定值?若是,请求出该定值;若不是,请说明理由;
的斜率之积是否为定值?若是,请求出该定值;若不是,请说明理由;
(2)求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4个不同的球,4个不同的盒子,把球全部放入盒子内.
(1)共有几种放法?
(2)恰有1个空盒,有几种放法?
(3)恰有2个盒子不放球,有几种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张师傅想要一个如图1所示的钢筋支架的组合体,来到一家钢制品加工店定制,拿出自己画的组合体三视图(如图2所示).店老板看了三视图,报了最低价,张师傅觉得很便宜,当即甩下定金和三视图,约定第二天提货.第二天提货时,店老板一脸坏笑的捧出如图3–1所示的组合体,张师傅一看,脸都绿了:“奸商,怎能如此偷工减料”.店老板说,我是按你的三视图做的,要不我给你加一个正方体,但要加价,随机加上了一个正方体,得到如图3–2所示的组合体;张师傅脸还是绿的,店老板又加上一个正方体,组成了如图 3–3 所示的组合体,又加价;张师傅脸继续绿,店老板再加一个正方体,组成如图 3–4 所示的组合体,再次加价;双方就三视图争吵不休……
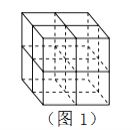
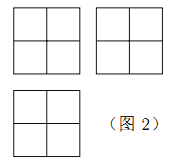
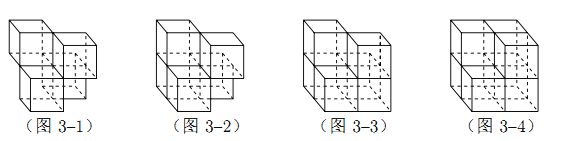
你认为店老板提供的![]() 个组合体的三视图与张师傅画的三视图一致的个数是( )
个组合体的三视图与张师傅画的三视图一致的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com