
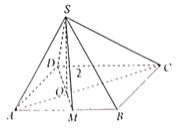
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证;平面![]() 平面
平面![]()
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,利用向量法证明
轴,建立空间直角坐标系,利用向量法证明![]() ,由
,由![]() 平面
平面![]() ,得出
,得出![]() ,结合直线与平面垂直的判定定理证明
,结合直线与平面垂直的判定定理证明![]() 平面
平面![]() ,最后由平面与平面垂直的判定定理证明平面
,最后由平面与平面垂直的判定定理证明平面![]() 平面
平面![]() ;
;
(2)计算出平面![]() 的一个法向量
的一个法向量![]() ,利用向量计算出向量
,利用向量计算出向量![]() 与
与![]() 的夹角的余弦值,取其绝对值作为直线
的夹角的余弦值,取其绝对值作为直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
(1)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() ,0,
,0,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() 面
面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]()
(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
则 ,取
,取![]() ,得
,得![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() .
.
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】中国国际智能产业博览会(智博会)每年在重庆市举办一届,每年参加服务的志愿者分“嘉宾”、“法医”等若干小组,![]() 年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出20人作为2019年中国国际智博会服务的志愿者.
年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出20人作为2019年中国国际智博会服务的志愿者.
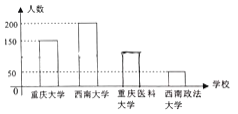
(1)分别求出从重庆大学、西南大学、重庆医科大学、西南政法大学抽出的志愿者人数;
(2)若“嘉宾”小组的2名志愿者只能从重庆医科大学或西南政法大学抽出,求这2人分别来自不同大学的概率(结果用分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
,![]() 为其焦点,椭圆
为其焦点,椭圆![]() ,
,![]() ,
,![]() 为其左右焦点,离心率
为其左右焦点,离心率![]() ,过
,过![]() 作
作![]() 轴的平行线交椭圆于
轴的平行线交椭圆于![]() 两点,
两点,![]() .
.
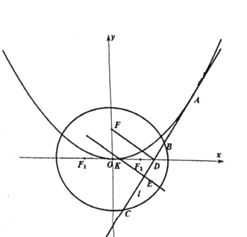
(1)求椭圆的标准方程;
(2)过抛物线上一点![]() 作切线
作切线![]() 交椭圆于
交椭圆于![]() 两点,设
两点,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中垂线交
的中垂线交![]() 轴为
轴为![]() ,
,![]() ,
,![]() 的面积分别记为
的面积分别记为![]() ,
,![]() ,若
,若![]() ,且点
,且点![]() 在第一象限.求点
在第一象限.求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
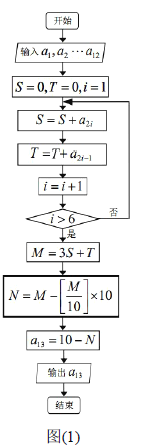
【题目】条形码是由一组规则排列的条、空及其对应的代码组成,用来表示一定的信息,我们通常见的条形码是“![]() ”通用代码,它是由从左到右排列的
”通用代码,它是由从左到右排列的![]() 个数字(用
个数字(用![]() ,
,![]() ,…,
,…,![]() 表示)组成,这些数字分别表示前缀部分、制造厂代码、商品代码和校验码,其中
表示)组成,这些数字分别表示前缀部分、制造厂代码、商品代码和校验码,其中![]() 是校验码,用来校验前
是校验码,用来校验前![]() 个数字代码的正确性.图(1)是计算第
个数字代码的正确性.图(1)是计算第![]() 位校验码的程序框图,框图中符号
位校验码的程序框图,框图中符号![]() 表示不超过
表示不超过![]() 的最大整数(例如
的最大整数(例如![]() ).现有一条形码如图(2)所示(
).现有一条形码如图(2)所示(![]() ),其中第
),其中第![]() 个数被污损,那么这个被污损数字
个数被污损,那么这个被污损数字![]() 是( )
是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存
,是否存![]() 在使得
在使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com