练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某社团组织名志愿者利用周末和节假日参加社会公益活动,活动内容是：1、到各社区宣传慰问,倡导文明新风；2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示：
     
    		宣传慰问
    		义工
    		总计
    20至40岁
    		11
    		16
    		27
    大于40岁
    		15
    		8
    		23
    总计
    		26
    		24
    		50
    (1) 分层抽样方法在做义工的志愿者中随机抽取6名,年龄大于40岁的应该抽取几名?
    (2) 上述抽取的6名志愿者中任取2名,求选到的志愿者年龄大于40岁的人数的数学期望.
    （1）2人;（2）.

    试题分析：(1)根据分层抽样中的比例关系得到第一问的结论（2）利用概率得到每种情况下的概率，列出分布列，利用期望的公式求出答案.
    试题解析：(1)若在做义工的志愿者中随机抽取6名,则抽取比例为     2分
    ∴ 年龄大于40岁的应该抽取人.                4分   
    (2)在上述抽取的6名志愿者中任取2名,假设选到年龄大于40岁的人数为,
    ∵  6名志愿者中有2人的年龄大于40岁,其余4人的年龄在20到40岁之间,
    ∴ 可能的取值为.                              5分
    则,,     8分
    ∴的分布列为








       10分
    ∴  的数学期望为         12分
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    生产A，B两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：
    测试指标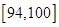





    元件A
    		8
    		12
    		40
    		32]
    		8
    元件B
    		7
    		18
    		40
    		29
    		6
    （1）试分别估计元件A、元件B为正品的概率；
    （2）生产一件元件A，若是正品可盈利50元，若是次品则亏损10元；生产一件元件B，若是正品可盈利100元，若是次品则亏损20元，在（1）的前提下；
    （i）求生产5件元件B所获得的利润不少于300元的概率；
    （ii）记X为生产1件元件A和1件元件B所得的总利润，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某项考试按科目A、科目B依次进行，只有当科目A成绩合格时，才可继续参加科目B的考试.已知每个科目只允许有一次补考机会，两个科目成绩均合格方可获得证书.现某人参加这项考试，科目A每次考试成绩合格的概率均为，科目B每次考试成绩合格的概率均为.假设各次考试成绩合格与否均互不影响.
    （1）求他不需要补考就可获得证书的概率；
    （2）在这项考试过程中，假设他不放弃所有的考试机会，记他参加考试的次数为，求 的分布列及数学期望E.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （14分）如图所示,机器人海宝按照以下程序运行

    1从A出发到达点B或C或D，到达点B、C、D之一就停止；
    ②每次只向右或向下按路线运行；
    ③在每个路口向下的概率；
    ④到达P时只向下，到达Q点只向右．
    （1）求海宝过点从A经过M到点B的概率，求海宝过点从A经过N到点C的概率；
    （2）记海宝到点B、C、D的事件分别记为X=1，X=2，X=3，求随机变量X的分布列及期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为了解甲、乙两厂产品的质量，从两厂生产的产品中分别随机抽取各10件样品，测量产品中某种元素的含量（单位：毫克）.如图是测量数据的茎叶图：

    规定：当产品中的此种元素含量不小于18毫克时，该产品为优等品.
    （1）试用上述样本数据估计甲、乙两厂生产的优等品率；
    （2）从乙厂抽出的上述10件样品中，随机抽取3件，求抽到的3件样品中优等品数的分布列及其数学期望；
    （3）从甲厂的10件样品中有放回的随机抽取3件，也从乙厂的10件样品中有放回的随机抽取3件，求抽到的优等品数甲厂恰比乙厂多2件的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为了整顿道路交通秩序，某地考虑将对行人闯红灯进行处罚．为了了解市民的态度，在普通行人中随机选取了200人进行调查，得到如下数据：
    处罚金额x(元)
    		0
    		5
    		10
    		15
    		20
    会闯红灯的人数y
    		80
    		50
    		40
    		20
    		10
    若用表中数据所得频率代替概率．现从这5种处罚金额中随机抽取2种不同的金额进行处罚，在两个路口进行试验．
    (Ⅰ)求这两种金额之和不低于20元的概率；
    (Ⅱ)若用X表示这两种金额之和，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    样本中共有5个个体，其值分别为.若该样本的平均值为1，则样本方差为
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某人上楼梯，每步上一阶的概率为，每步上二阶的概率为，设该人从台阶下的平台开始出发，到达第阶的概率为.
    (1)求；;
    (2)该人共走了5步，求该人这5步共上的阶数ξ的数学期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列是随机变量ξ的分布列







    		x
    则随机变量ξ的数学期望是
    A．0.44                B．0.52            C．1.40        D．条件不足

    查看答案和解析>>

    同步练习册答案