解:(1)点(kπ,0)(k∈Z)是正弦曲线的对称中心,由正弦曲线的性质知,此命题是正确命题;
(2)点(0,0)是余弦曲线的一个对称中心,余弦曲线的对称中心是(kπ+

,0)(k∈Z),故此命题不对;
(3)把余弦函数y=cosx的图象向左平移

个单位得到y=cos(x+

)=-sinx,得不到y=sinx的图象,此命题错误;
(4)在余弦曲线y=cosx中,最高点与它相邻的最低点的水平距离是π,半个周期,不是2π,此命题错误;
(5)在正弦曲线y=sinx中,相邻两个最高点的水平距离是2π,此时正确命题,两个最高点之间的距离正好是一个周期.
综上知,(1)(5)是正确命题
故答案为,(1)(5)
分析:(1)点(kπ,0)(k∈Z)是正弦曲线的对称中心,由正弦曲线的对称性验证即可;
(2)点(0,0)是余弦曲线的一个对称中心,由余弦曲线的对称性验证;
(3)把余弦函数y=cosx的图象向左平移

个单位,即得y=sinx的图象,可由诱导公式验证;
(4)在余弦曲线y=cosx中,最高点与它相邻的最低点的水平距离是2π,由余弦曲线的性质验证;
(5)在正弦曲线y=sinx中,相邻两个最高点的水平距离是2π,由正弦曲线的性质进行验证.
点评:本题考查正弦函数的对称性,解题的关键是对正、余弦函数的性质有一个全面的了解,本题主要涉及到两个函数的图象本身的对称性及两个函数图象之间的关系.

 个单位,即得y=sinx的图象;(4)在余弦曲线y=cosx中,最高点与它相邻的最低点的水平距离是2π;(5)在正弦曲线y=sinx中,相邻两个最高点的水平距离是2π.其中正确的命题的序号是________.
个单位,即得y=sinx的图象;(4)在余弦曲线y=cosx中,最高点与它相邻的最低点的水平距离是2π;(5)在正弦曲线y=sinx中,相邻两个最高点的水平距离是2π.其中正确的命题的序号是________. ,0)(k∈Z),故此命题不对;
,0)(k∈Z),故此命题不对; 个单位得到y=cos(x+
个单位得到y=cos(x+ )=-sinx,得不到y=sinx的图象,此命题错误;
)=-sinx,得不到y=sinx的图象,此命题错误; 个单位,即得y=sinx的图象,可由诱导公式验证;
个单位,即得y=sinx的图象,可由诱导公式验证;

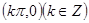 是正弦曲线的对称中心;(2)点
是正弦曲线的对称中心;(2)点 是余弦曲线的一个对称中心;(3)把余弦函数
是余弦曲线的一个对称中心;(3)把余弦函数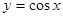 的图像向左平移
的图像向左平移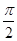 个单位,即得
个单位,即得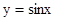 的图像;(4)在余弦曲线
的图像;(4)在余弦曲线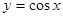 中,最高点与它相邻的最低点的水平距离是
中,最高点与它相邻的最低点的水平距离是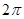 ;(5)在正弦曲线
;(5)在正弦曲线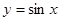 中,相邻两个最高点的水平距离是
中,相邻两个最高点的水平距离是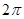 。其中正确的命题的序号是___
。其中正确的命题的序号是___