
设函数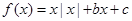 ,给出下列四个命题:
,给出下列四个命题:
①当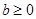 时,函数
时,函数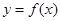 是单调函数
是单调函数
②当 时,方程
时,方程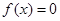 只有一个实根
只有一个实根
③函数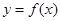 的图象关于点
的图象关于点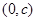 对称
对称
④方程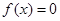 至多有3 个实根,其中正确命题的个数为
至多有3 个实根,其中正确命题的个数为
A.1个 B.2个 C.3个 D.4个
D
【解析】
试题分析:因为f(x)=x|x|+bx+c=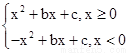 ,对于①当x≥0时,f'(x)=2x+b≥0,所以y=f(x)递增,当x<0时,f'(x)>0,所以y=f(x)递增又y=f(0)=c连续.故当b≥0时,函数y=f(x)是单调函数; ①对.
,对于①当x≥0时,f'(x)=2x+b≥0,所以y=f(x)递增,当x<0时,f'(x)>0,所以y=f(x)递增又y=f(0)=c连续.故当b≥0时,函数y=f(x)是单调函数; ①对.
对于②因为f(x)=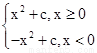 当x≥0时无根,当x<0时,有一根x=-
当x≥0时无根,当x<0时,有一根x=-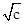 .故当b=0,c>0时,方程f(x)=0只有一个实根;②对.
.故当b=0,c>0时,方程f(x)=0只有一个实根;②对.
对于③设g(x)=x|x|+bx,因为g(-x)=-x|-x|+b(-x)=-g(x),所以g(x)=x|x|+bx关于(0,0)对称,又函数y=f(x)的图象可以由g(x)=x|x|+bx的图象上下平移c个单位得到.故函数y=f(x)的图象关于点(0,c)对称;故③对.
对于④分各种情况来讨论b,c,并求出对应方程的根,就可说明④成立.故④对.
故选 D.
考点:本试题主要考查了对带绝对值的二次函数的综合考查.
点评:解决该试题的关键是通常带绝对值的函数研究其性质时,要去掉其绝对值符号进行. ①去掉其绝对值符号,判断出其在每一段内都单调且连续即可.
②把b=0,c>0代入,去掉其绝对值符号,解对应方程即可得结论.
③利用g(x)=x|x|+bx关于(0,0)对称,和g(x)=x|x|+bx与y=f(x)的关系可得结论.
④对于b,c分各种情况来讨论,并求出对应方程的根,可下结论


科目:高中数学 来源: 题型:
设函数![]() ,给出下列四个命题:①
,给出下列四个命题:①![]() 时,
时,![]() 是奇函数②
是奇函数②![]() ,时,方程
,时,方程![]() 只有一个实根③
只有一个实根③![]() 的图像关于
的图像关于![]() 对称④方程
对称④方程![]() 至多有两个实根。其中正确的命题是
至多有两个实根。其中正确的命题是
A.①④ B.①③ C.①②③ D.①②④
查看答案和解析>>
科目:高中数学 来源:2015届重庆第49中学七校联盟高一上学期期中考试数学试卷(解析版) 题型:选择题
设函数 ,给出下列四个命题:
,给出下列四个命题:
① 时,
时, 是奇函数 ②
是奇函数 ② 时,方程
时,方程 只有一个实根
只有一个实根
③ 的图象关于
的图象关于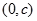 对称 ④方程
对称 ④方程 至多两个实数根
至多两个实数根
其中正确的命题的个数是( )
A.1 B. 2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2012-2013学年内蒙古巴彦淖尔市高三9月月考理科数学试卷(解析版) 题型:填空题
设函数 ,给出下列四个命题:
,给出下列四个命题:
① 时,
时, 是奇函数;
是奇函数;
② 时,方程
时,方程 只有一个实根;
只有一个实根;
③ 的图象关于
的图象关于 对称;
对称;
④方程 至多有两个实根。
至多有两个实根。
其中正确的命题序号是 ___________________________.
查看答案和解析>>
科目:高中数学 来源:2013届海南省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设函数 ,给出下列四个命题:
,给出下列四个命题:
① 时,
时, 是奇函数 ②
是奇函数 ② 时,方程
时,方程 只有一个实根
只有一个实根
③ 的图象关于点
的图象关于点 对称 ④方程
对称 ④方程 至多两个实根
至多两个实根
其中正确的命题是( )
A.①④ B.①③ C.①②③ D.①②④
查看答案和解析>>
科目:高中数学 来源:2011-2012年黑龙江省高一上学期期中考试数学 题型:选择题
设函数 ,给出下列四个命题:
,给出下列四个命题:
(1)
当 时,函数
时,函数 是单调函数;
是单调函数;
(2)
当 时,方程
时,方程 只有一个实根
只有一个实根
(3)
函数 的图像关于点
的图像关于点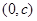 对称;
对称;
(4)
方程 至多有3个实根
至多有3个实根
其中正确命题的个数是( )
A、1个 B、2个 C、3个 D、4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com