
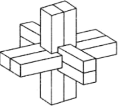
【题目】鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.从外观上看,是严丝合缝的十字立方体,其上下、左右、前后完全对称;六根等长的正四棱柱分成三组,经90°榫卯起来.如图所示,正四棱柱的高为8,底面正方形的边长为1,将这个鲁班锁放进一个球形容器内,则该球形容器半径的最小值为(容器壁的厚度忽略不计)( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中, AB=2,BD=![]() ,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.
,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.

(1)求AD的长;
(2)求△CBD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() (
(![]() )的焦点是椭圆
)的焦点是椭圆![]() :
: ![]() (
(![]() )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点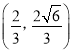
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
, ![]() ,若过点
,若过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相较于点
相较于点![]() ,试判断点
,试判断点![]() 是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了改善空气质量,某市规定,从2018年1月1日起,对二氧化碳排放量超过![]() 的轻型汽车进行惩罚性征税.检测单位对甲乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下:(单位:
的轻型汽车进行惩罚性征税.检测单位对甲乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下:(单位:![]() )
)
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 |
| 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为![]() .
.
(1)求表中![]() 的值,并比较甲乙两品牌轻型汽车二氧化碳排放量的稳定性;
的值,并比较甲乙两品牌轻型汽车二氧化碳排放量的稳定性;
(2)从被检测的5辆甲品牌汽车中随机抽取2辆,求至少有1辆二氧化碳排放量超过![]() 的概率.(注:方差
的概率.(注:方差![]() ,其中
,其中![]() 为
为![]() 的平均数).
的平均数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:①若“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②若“![]() ,
,![]() ”,则实数
”,则实数![]() 的取值范围是
的取值范围是![]() ;
;
③已知平面![]() 、
、![]() 、
、![]() ,直线
,直线![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④函数![]() 的所有零点存在区间是
的所有零点存在区间是![]() .
.
其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率都是40%.现采用随机模拟的方法估计该运动员三次投篮恰有一次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数作为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907,966,191,925,271,932,812,458,569,683,431,257,393,027,556,488,730,113,537,989.据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.25B.0.2C.0.35D.0.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() ,且直线
,且直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在开展学习强国的活动中,某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有4名男教师、1名女教师,非党员学习组有2名男教师、2名女教师,高三数学组计划从两个学习组中随机各选2名教师参加学校的挑战答题比赛.
(1)求选出的4名选手中恰好有一名女教师的选派方法数;
(2)记X为选出的4名选手中女教师的人数,求X的概率分布和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com