
【题目】已知函数![]() (
(![]() ,
,![]() )的最小正周期是
)的最小正周期是![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后所得的函数为
个单位长度后所得的函数为![]() ,则函数的
,则函数的![]() 图象( )
图象( )
A. 有一个对称中心![]() B. 有一条对称轴
B. 有一条对称轴![]()
C. 有一个对称中心![]() D. 有一条对称轴
D. 有一条对称轴![]()
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. 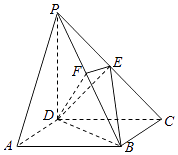
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论: ①已知函数f(x)是定义在R上的奇函数,若f(﹣1)=2,f(﹣3)=﹣1,则f(3)<f(﹣1);
②函数y=log ![]() (x2﹣2x)的单调递增减区间是(﹣∞,0);
(x2﹣2x)的单调递增减区间是(﹣∞,0);
③已知函数f(x)是奇函数,当x≥0时,f(x)=x2 , 则当x<0时,f(x)=﹣x2;
④若函数y=f(x)的图象与函数y=ex的图象关于直线y=x对称,则对任意实数x,y都有f(xy)=f(x)+f(y).
则正确结论的序号是(请将所有正确结论的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对营销人员有如下规定:
①年销售额![]() (万元)在8万元以下,没有奖金;
(万元)在8万元以下,没有奖金;
②年销售额![]() (万元),
(万元), ![]() 时,奖金为
时,奖金为![]() 万元,且
万元,且![]() ,
, ![]() ,且年销售额越大,奖金越多;
,且年销售额越大,奖金越多;
③年销售额超过64万元,按年销售额的10%发奖金.
(1)求奖金y关于x的函数解析式;
(2)若某营销人员争取奖金![]() (万元),则年销售额
(万元),则年销售额![]() (万元)在什么范围内?
(万元)在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
(1)随机误差e是衡量预报精确度的一个量,它满足E(e)=0
(2)残差平方和越小的模型,拟合的效果越好;
(3)用相关指数R2来刻画回归的效果时,R2的值越小,说明模型拟合的效果越好;
(4)直线y=bx+a和各点(x1 , y1),(x2 , y2),…,(xn , yn)的偏差 ![]() 是该坐标平面上所有直线与这些点的偏差中最小的直线.
是该坐标平面上所有直线与这些点的偏差中最小的直线.
其中真命题的个数( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2﹣(a+1)x+1
(1)解关于x的不等式f(x)>0;
(2)若对任意的a∈[﹣1,1],不等式f(x)>0恒成立,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com